lec23 Shortest Paths

引入

BFS 只会考虑边的个数。如果每个边有不同的长度，那么就不能简单地使用 BFS。

显然，最佳的路径不会有圈。

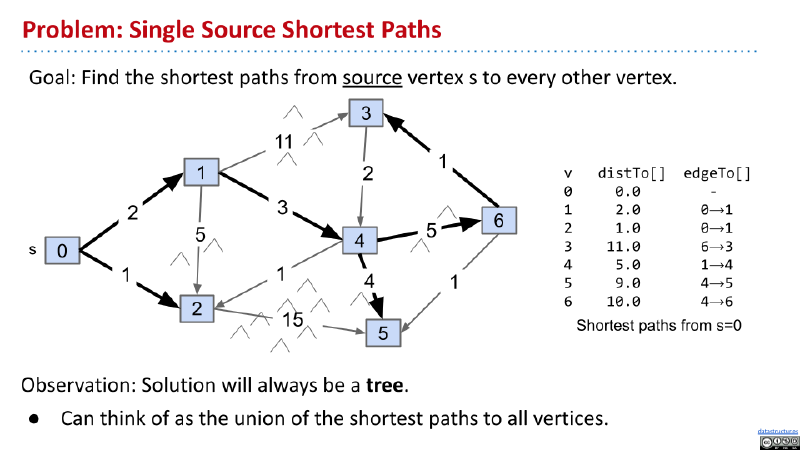
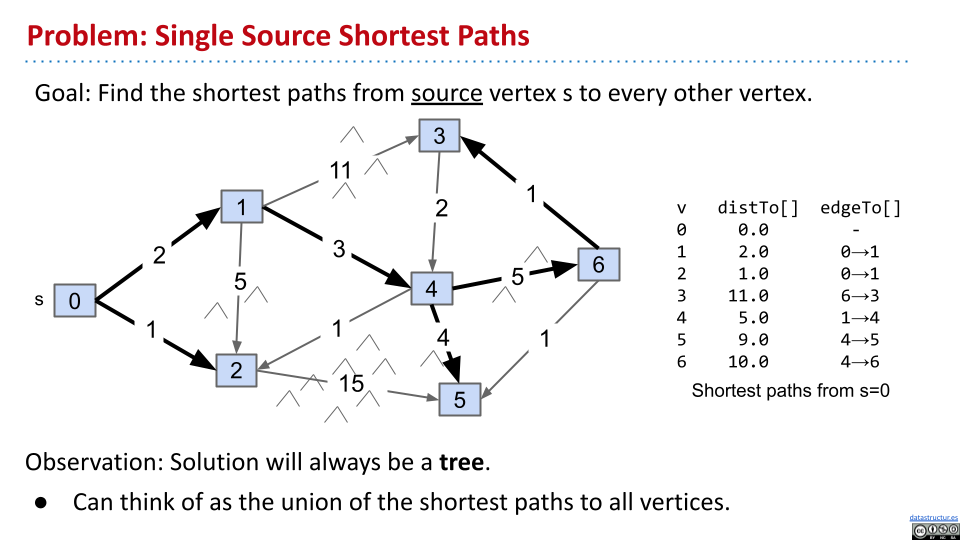很有趣的是，最后各个节点的最优路径会形成一棵树。包括有向图和无向图。这个路径成为 Shortest Path Tree（SPT）。

在 SPT 中，边的个数总数 V-1，V 为节点的个数。

尝试

第一个算法

一开始所有节点的距离设置为无穷。然后进行深度优先搜索，对于相邻每个节点，如果不在 SPT 中，就加入这个边。然而，这样无法得到最短的路径，因为只要有节点被标记，就不再遍历相应的边。

第二个算法

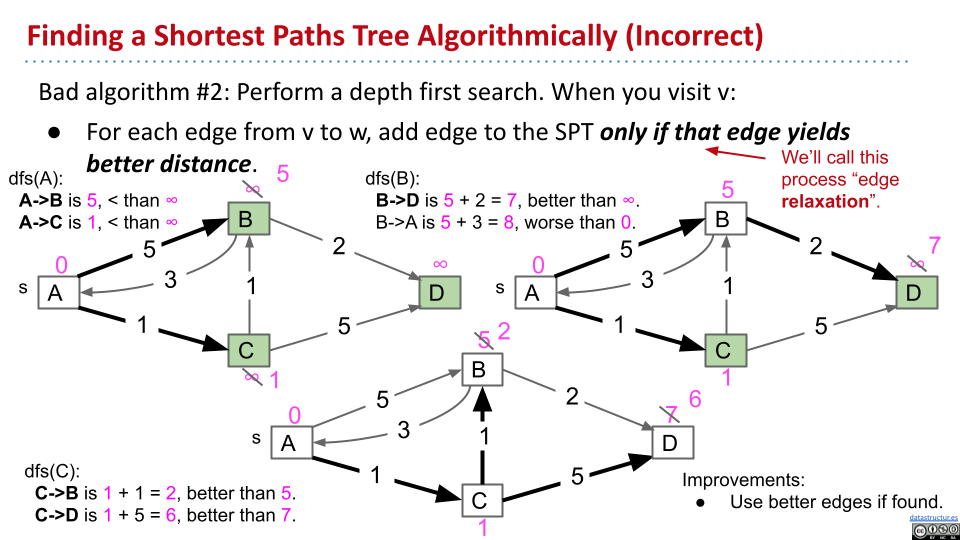
利用深度优先搜索，如果某个边可以产生更短的距离，就将这个边加入 SPT。在这个例子中，考虑 C 之后应该重新考虑 B，才有可能得到最短路径。

Dijkstra

不要用深度优先，而是用"best first search"。

在每一次选择下一个遍历的节点时，聚焦于距离最短的那个节点。然后，计算各个边带来的距离，并且更新最短距离。

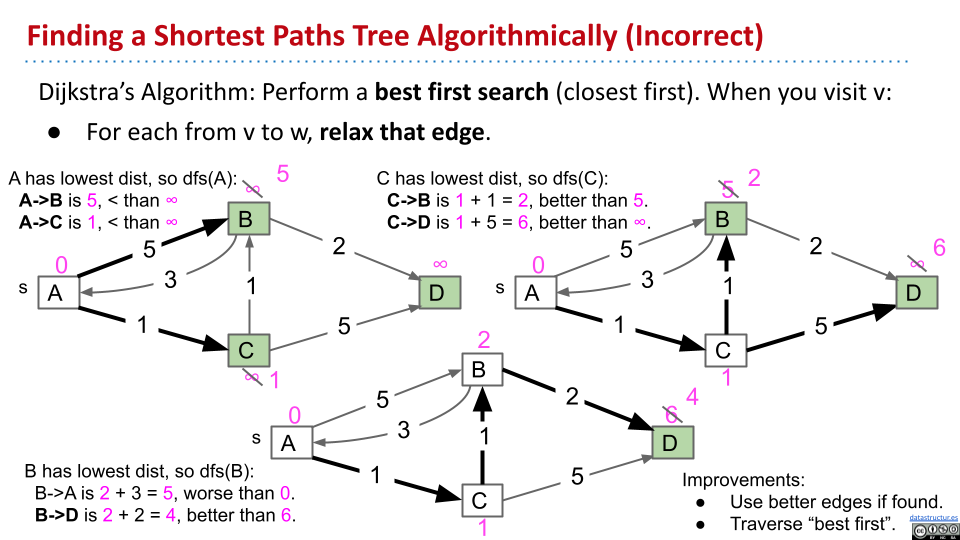
将所有的点插入 fringe PQ，储存节点距离源的距离。重复以下步骤：

• 从 PQ 中移除距离最小的节点
• 更新该节点指向的所有边，包括 distTo 和 edgeTo

lec24 Minimum Spanning Trees

引入

如何判断一个图当中是否有圈？

一：使用 DFS。从某个节点开始，直到遇到标记过的节点，但是不包括刚刚来的节点。最差情况是 $\Theta(V+E)$

二：使用并查集。对于每条边，检查两个节点是否相连。如果没有，就连接。如果有，就代表有环。最差情况为 $O(V+E\log*(V))$

最小生成树

只在无向图中存在。生成树是图的一个子集，包含所有节点，并且是连接、无环的。最小生成树意味着每条边的值加起来最小，即 MST。

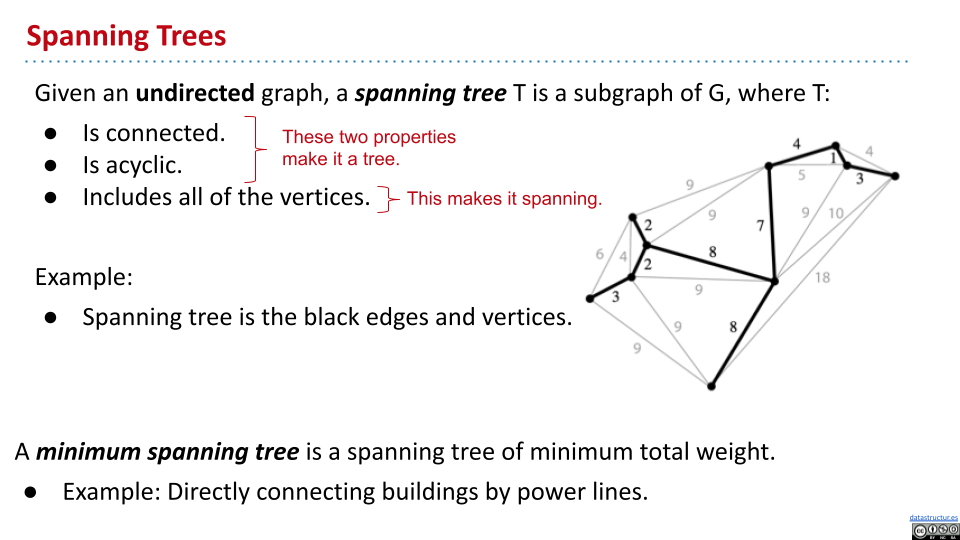
在有些图中，从某些节点出发的 SPT 并不是 MST，但有些节点是。但有些图中，根本没有 SPT 是 MST。所以，不能通过先确定某个节点，再根据 Dijkstra 来找到 MST。

Cut 特性

Cut 将图中节点分类两类非空集合。一个交叉边就是连接两个不同集合节点的边。Cut 特性：给定任意的 Cut，拥有最小值的交叉边一定是 MST 的一部分。这可以通过反证法证明。

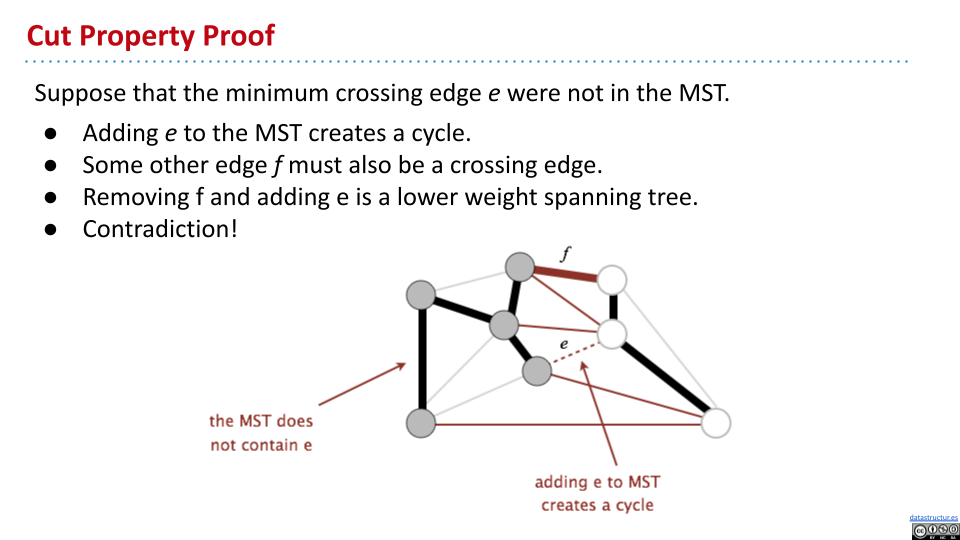
利用这个，可以找到一个 cut，它的交叉边都不在 MST 中，然后将最小值加入 MST。不断重复。

Prim 算法

第一次选取最短的边。然后考虑所有标记过的节点，将其和剩余节点看做一个 cut，然后找到最小值的边。当有两个相同最小值时，选择任意一个都行。有时候，MST 不是唯一的。

为了让 Prim 算法更高效，在 PQ 中储存节点距离树的距离。然后，找到最小的，将这个点从 fringe 中移除。

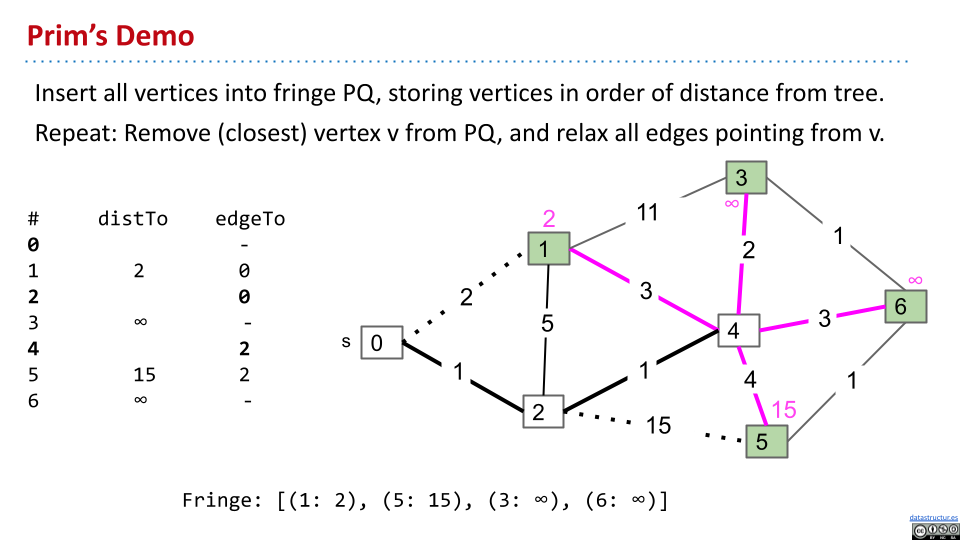
Dijkastra 考虑距离起点的距离，Prim 考虑距离树的距离。

在 E 大于 V 的情况下，时间复杂度为 $O(E\log(V))$。

Kruskal 算法

将所有边排序，从小的开始。如果加入后不导致成环，那就加入。与 Prim 不同，这个在过程中并不一定是互相连接的。

每次考虑最小边，将该节点在的一个树与剩余部分看成 Cut，根据性质，最小边在 MST 当中。

在实现中，为了判断成环，可以使用并查集。如果当前边对应节点在并查集中不相连，就连接两个节点；否则，说明成环，不能加入该边。为了追踪最小边，使用 PQ。

最终的消耗的时间主要取决于将所有边从 PQ 的加入、删除的时间，也就是 $O(E\log(E))$。不过，如果已经知道了图中各个边的大小次序，那么运行时间主要取决于并查集的速度，需要进行 E 次连接、是否连接的操作，总时间缩减到 $O(E\log*V)$。

lec25 Multidimentional data

多维数据引入

对于多维数据，不能简单地使用一个 BST 达到方便搜索的目的。例如对于有 x、y 坐标的对象，如果使用 x 坐标来构建二叉树，那么可以很方便地找到 x 坐标小于 1.5 的点。

通过剪枝，可以减少需要搜索的情况。

多叉树

四叉树

不像二叉树一样只有两个子节点，四叉树有四个节点，表示在二维空间中四种位置关系。和二叉树一样，不同的插入顺序会影响树的性能。

这时，要进行矩形的搜索更方便。如果矩形在某一点的四个区域之内，就可以对剩下的区域进行剪枝。

三维数据

类似地，可以使用八叉树。

然而，当维度更高的时候，使用这种思想就不太行，空间会呈指数型增长。

K-D 树

如果维度为 2，那么根节点根据 x 分类；深度为 1 的节点通过 y 分类；深度为 2 的节点通过 x 分类。以此类推。

有时候，如果发现数值相同，需要打破平衡，例如进入右子节点。

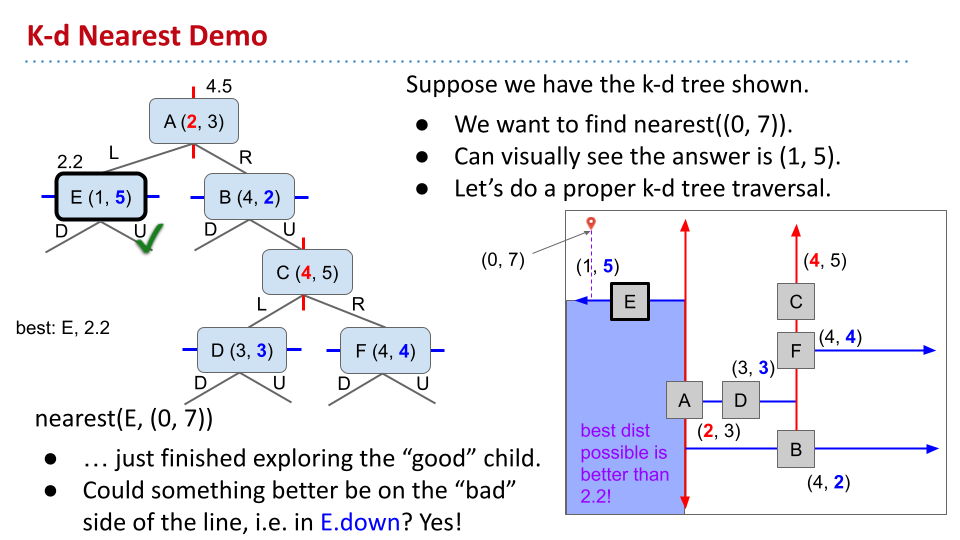
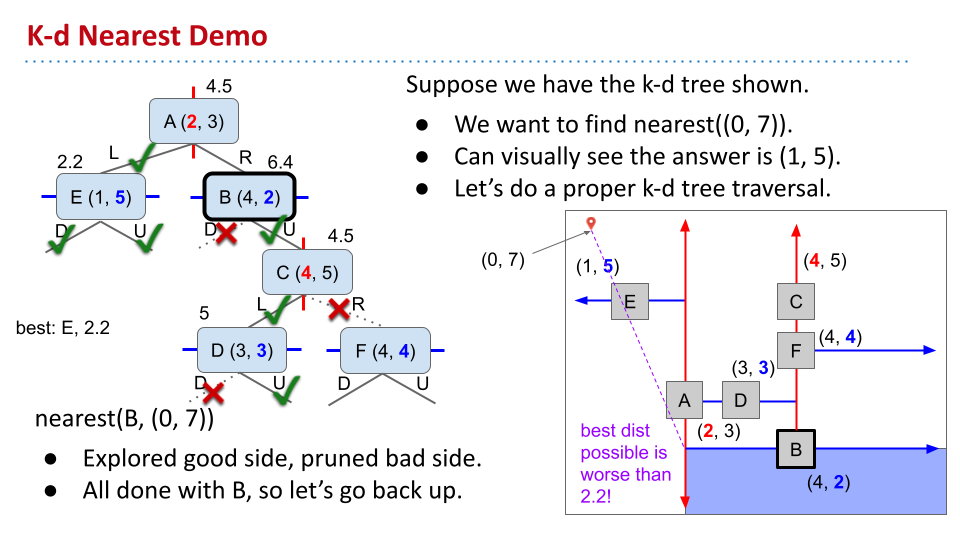
在寻找距离某个点最近的节点时，也可以使用 k-d 树方便地通过遍历，直到最近节点所在的区域。需要注意，还需要在之前没考虑的区域考虑。这种考虑也要靠近更好的区域。在之后考虑更差的区域时，判断该区域最优情况下的距离是否好于当前值。如果不是，可以剪枝。

均匀分割

将空间分成多个 buckets。在矩形搜索中，只用看在矩形之中的 buckets。不过，性能会比不上四叉树或 k-d 树。

均匀分割的思想和 hashing 比较像。