Featured image of post CS61B week8 学习笔记
CS

CS61B week8 学习笔记

包括第八周讲座内容和lab8

lec20 Heaps and PQs

Priority Queue 接口

拥有以下四个方法：

  • void add(Item x)，将物品 x 加入 PQ
  • Item getSmallest() 返回 PQ 中最小的物品
  • Item removeSmallest() 移除并返回 PQ 中最小的物品
  • int size() 返回 PQ 物品的数量

任务

需要从 N 个消息中，找出最负面的 M 个消息。

一种显而易见的做法，就是先将 N 个消息根据负面程序排序，然后找出前 M 个最负面的。这在空间上会使用 $\Theta(N)$ 的内存。

如何利用 MinPQ，仅仅使用 $\Theta(M)$ 的内存呢？

一开始正常加入。如果物品超过了 M，每次都移除最小的元素。之后，就只有满足需求的 M 个物品。

不同的实现方法： lec20-1.png

理论上，平衡 BST 效果较好，然而算法较为复杂，同时不能储存多个相同值的物品。

Heap

Binary min-heap：完全的二叉树，并且每一个节点小于等于它的子节点。 lec20-2.png

对于堆来说，获得最小元素相当简单，就是根节点的值。

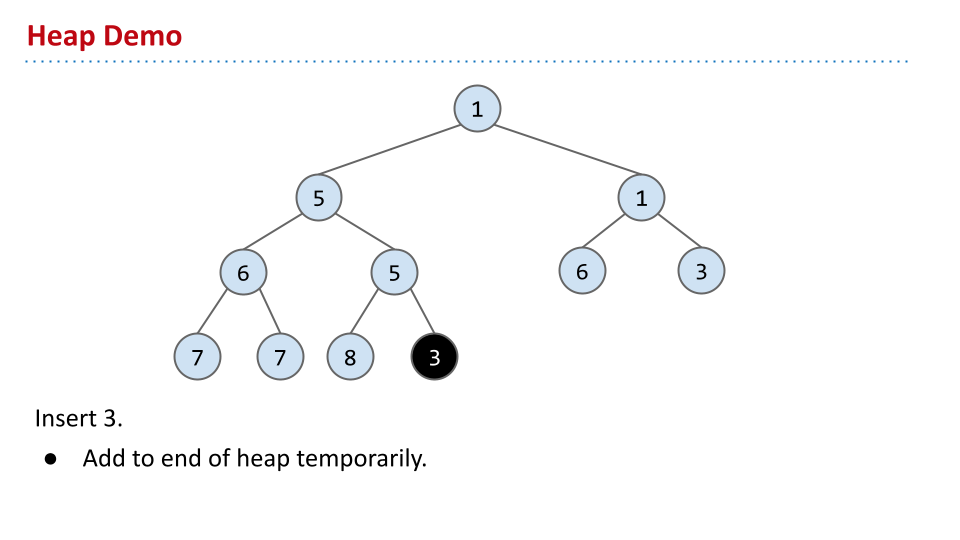
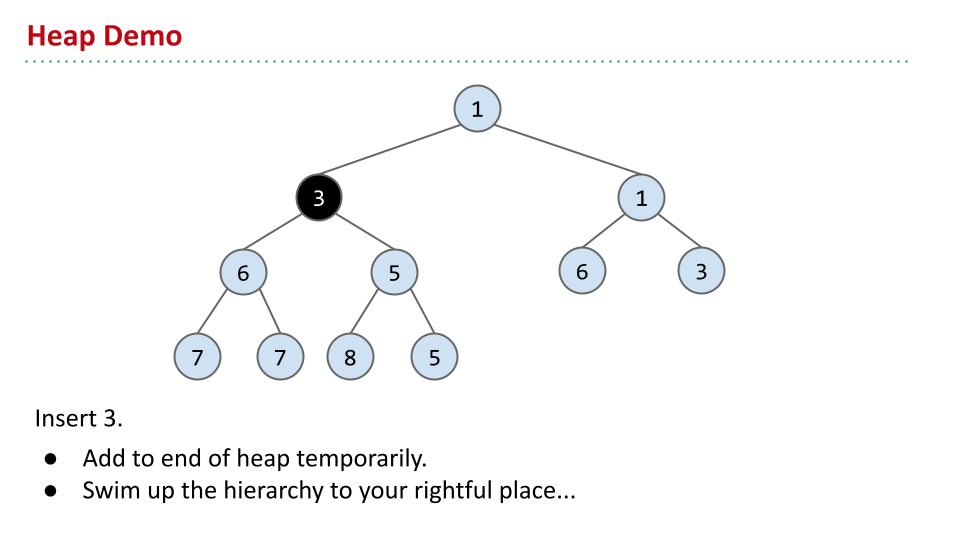
如果要插入，首先需要保证完备性。之后，将节点不断上爬，直到保证该节点大于等于父节点。如图： lec20-3.png lec20-4.png

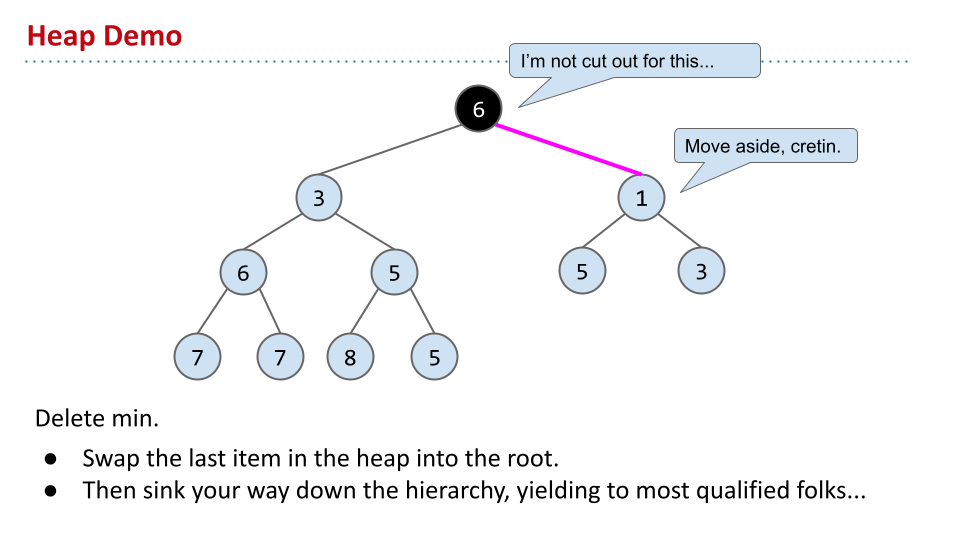
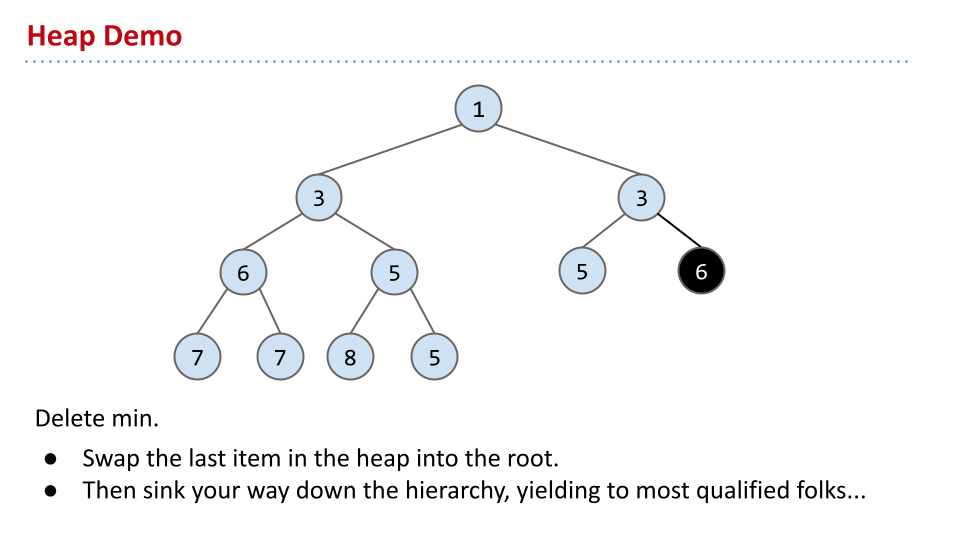
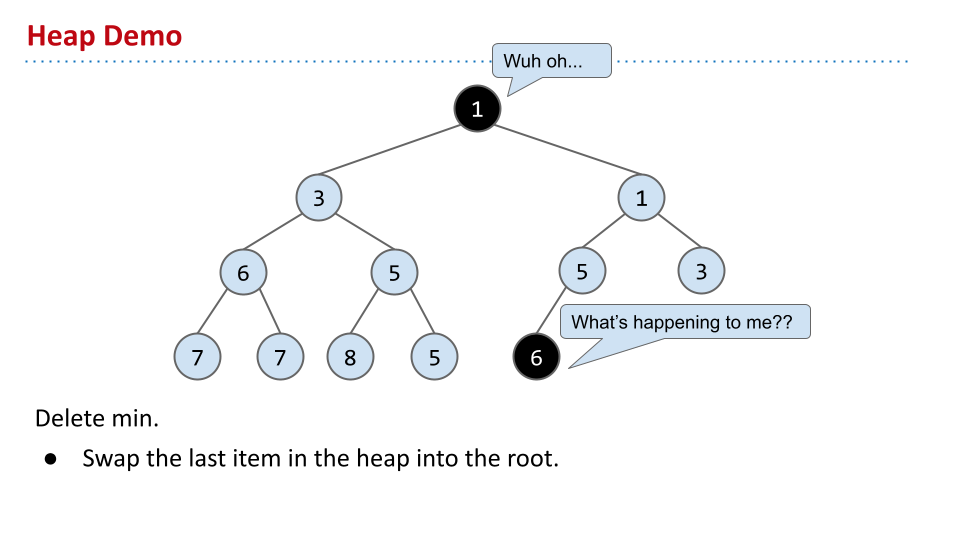
如果要删除最小值，根据完整性，首先让最后一层的最右侧填充根节点。然而，这不满足大小，因此不断与子节点交换，直到满足特性。 lec20-5.png lec20-6.png lec20-7.png

Tree 的表示

1

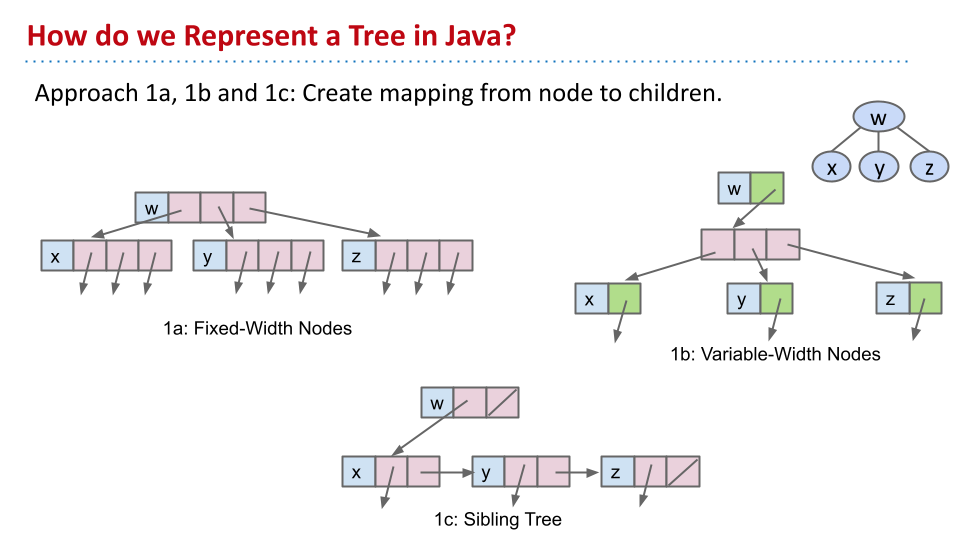
A： 每个节点拥有值 key，同时拥有多个子节点的指针。

B： 不是直接的拥有多个子节点的指针，而是有一个指针数组，每个分别指向一个子节点。缺点是代码更麻烦，性能可能下降。

C： Sibling Tree，一个指针指向下一层第一个节点，另一个指针指向 sibling。 lec20-8.png

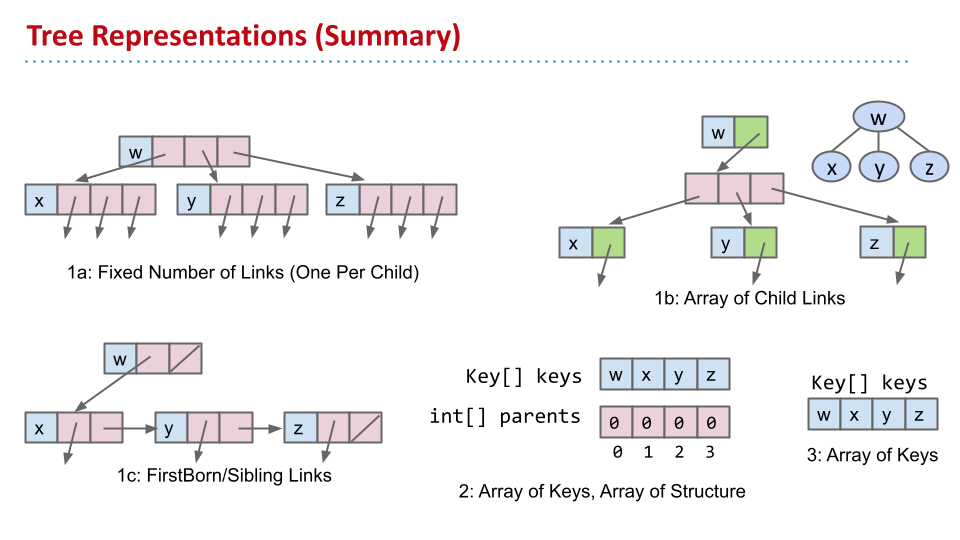
2

用一个数组来储存 keys，用另一个数组来储存 parents。在并查集当中就是这么做的。

3 a

在完全二叉树中，只使用一个数组来存储值。

为了寻找某个节点的父节点，可以使用当前节点的 $k$ 进行运算，得到 $(k-1)/2$。根据 Java 整数除法，这样就可以得到父节点的索引。 lec20-9.png

3 b

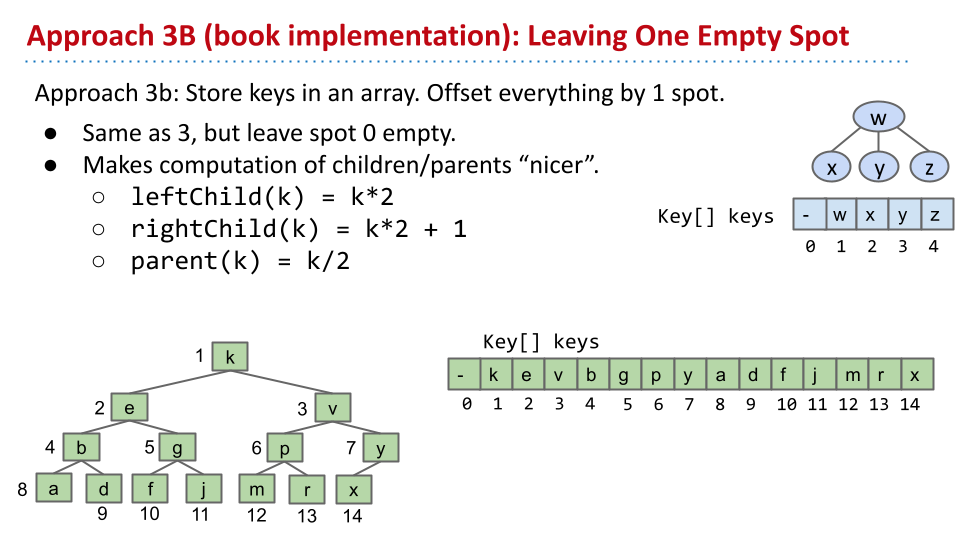
留出第一个空间，这样表达父节点、子节点很简单。 lec20-10.png lec20-11.png

数据结构总结

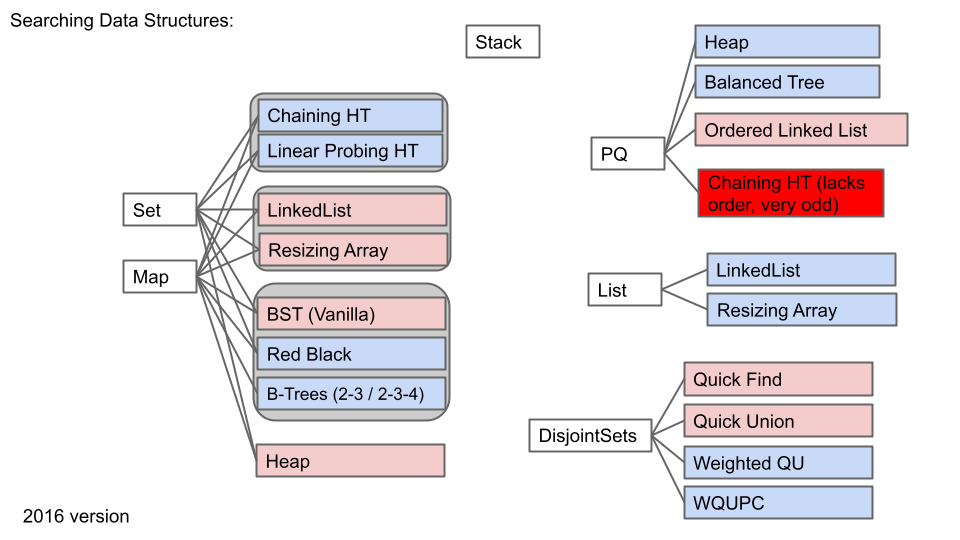
搜索问题：拥有大量数据，希望找到有用的信息。 lec20-12.png

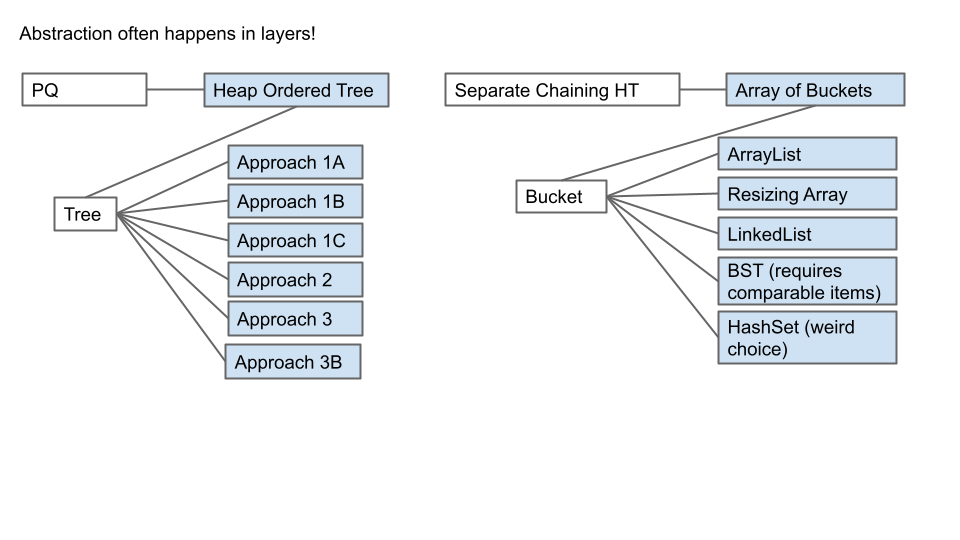
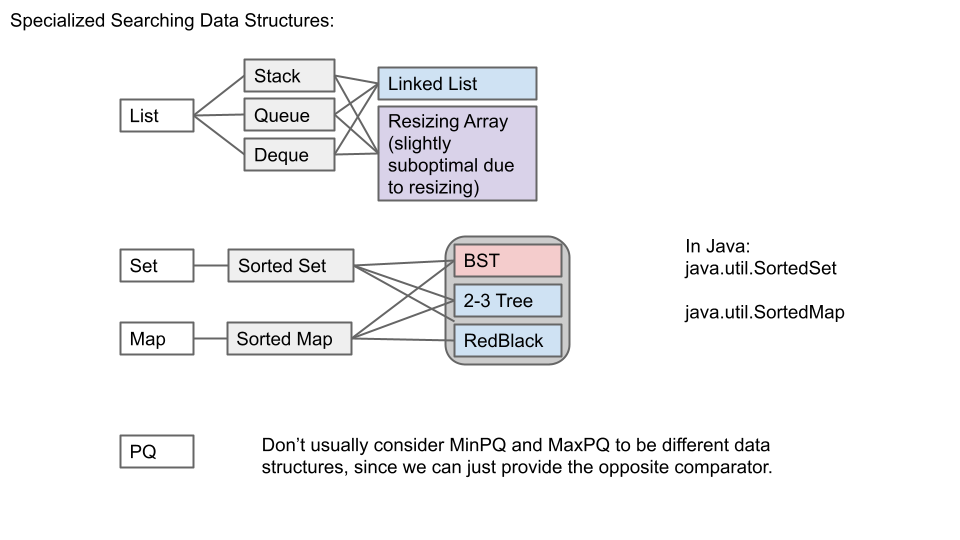
抽象往往有多个层次。例如对于 heap 树，也有多种实现的方法。 lec20-13.png lec20-14.png

数据结构就是整理数据的一种特殊方法。

lec21 Graphs and Traversals

树的遍历

树有许多种形式，包括公司中的组织结构，一个物种的树，文件系统等等。

很多时候，需要遍历树，即 tree traversal。

层序遍历

先遍历完第一层，再遍历完第二层，以此类推。

深度优先遍历

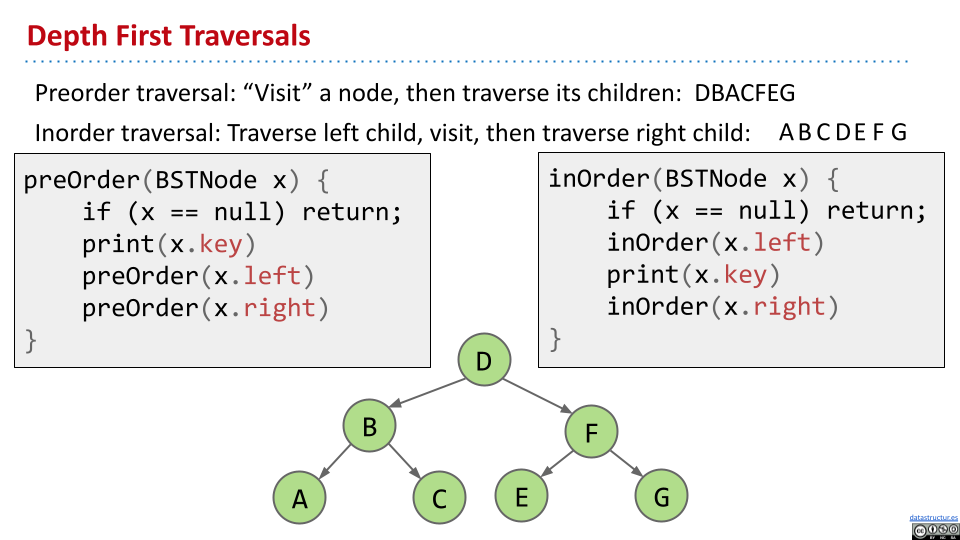
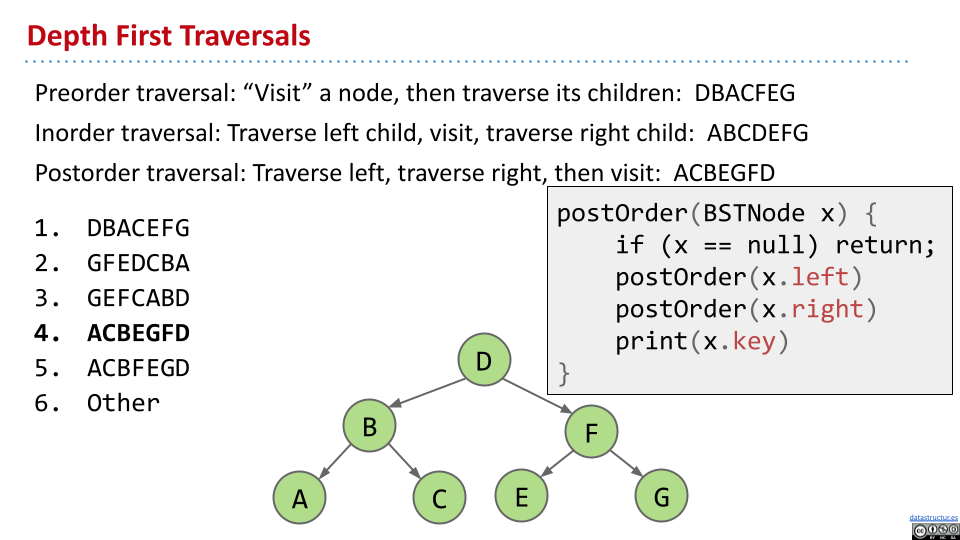
分为三种：前序、中序和后序。 lec21-1.png lec21-2.png

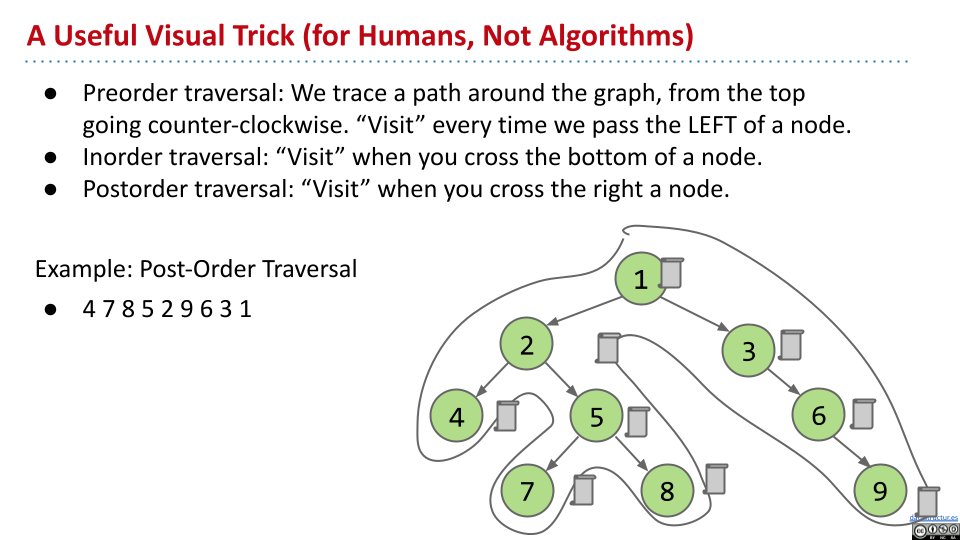
通过直观的方式，可以方便理解。从根节点开始，逆时针画一个圈包裹树。对于前序遍历，就访问每次路径在节点左侧的节点。对于中序遍历，就访问每次路径经过底部的节点。对于后序遍历，就访问每次路径经过右侧的节点。 lec21-3.png

图

定义

在图当中，两个节点之间可以有多个路径，并且可以有圈。

简单图：

  • 没有边会连接到自身节点。
  • 没有两条边会连接两个相同的节点。

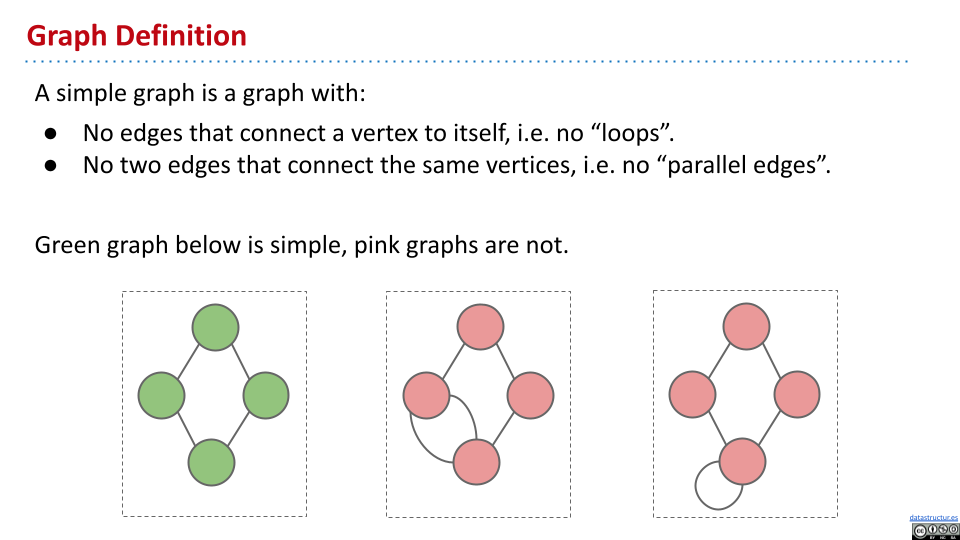lec21-4.png 通常，算法中涉及到的图都是简单图，因此之后说“图”的时候默认是“简单图”。

  • 有向图和无向图：边是否有方向。
  • 循环图：能否通过边来回到原先的节点。
  • 路径：一系列由边连接的节点。
  • 相连：如果两点之间有路径，就成为相连。
  • 图是相连：所有点之间都是相连的。

图的问题

  • 两点之间最短的路径是什么？最长的没有循环的路径是什么？
  • 是否有环？
  • 是否可以经过所有节点？
  • 是否可以经过所有的边？

常见问题：

  • S-t Path：s 和 t 之间是否有路径
  • Connectivity：图是否是相连的
  • Bioconnectivity：是否某个节点移除后，导致图不相连？
  • Shortest s-t Path：找出 s 和 t 之间的最短路径
  • Cyle Detection：是否有环
  • Euler Tour：是否有环可以刚好使用所有边一次
  • Hamilton Tour：是否有环可以刚好使用所有节点
  • Planarity：是否可以在二维平面上没有交叉的边
  • Isomorphism：两个图是否同构

有些图的问题很难解决，且不同问题难度相差极大。例如 Euler tour 在 1873 年就解决了，而今天 Hamilton Tour 也没有高效的算法，最好的算法也需要指数时间。

深度优先

S-t Connectivity

如果直接用递归，会出现无限循环。因此，每次经过某个节点 s，就标记 s，之后只搜索没有标记过的节点。此处有 demo lec21-5.png

寻找路径

通过深度优先，也可以找到从一个节点，到剩下所有节点的路径（不是最短的）。

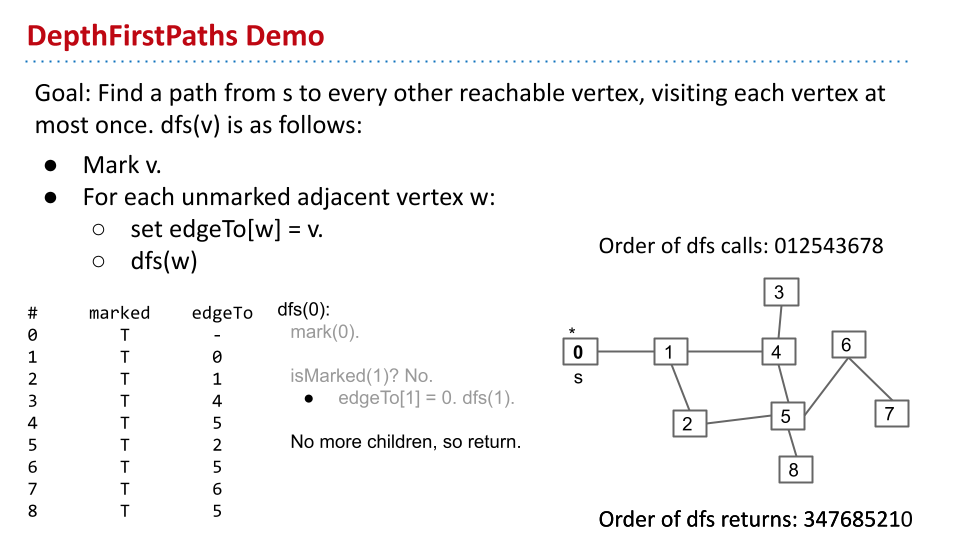
为了储存路径，设置一个新的数组 edgeTo，保存着当前路径的上一个节点。通过 marked 和 edgeTo，可以遍历图，找到路径。 lec21-8.png

图与树遍历的区别和联系

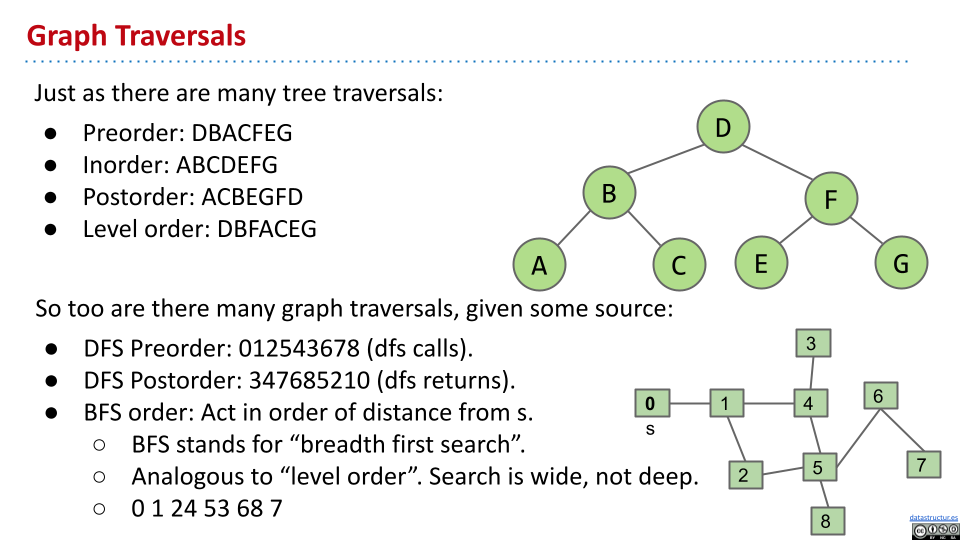
在树当中的前序、中序和后序，都相当于图当中的深度优先。图当中深度优先的前序，是每次经过一个节点，就打印出来。图当中深度优先的后序，可以理解为每一次阶数一个查找，要返回的时候，再打印出相应的节点。 lec21-7.png

与树当中的层级遍历类似，图当中也可以由广度优先搜索。

lec22 Graph Traversals and Implementations

广度优先

为了实现广度优先算法，需要使用队列。将队列称为 fringe。

  • 将节点 v 加入队列
  • 对于每一个没有标记的 v 的邻居 n:
    • 标记 n
    • 更新路径 edgeTo[n]=v
    • 更新距离 distTo[n]=distTo[v]+1
    • 将 n 加入队列
  • 之后在队列中去除 v

Graph API

需要决定图的 API，以及相应的底层数据结构。

整数节点

对于非整数节点，可以使用一个 Map 将其他元素映射到整数。

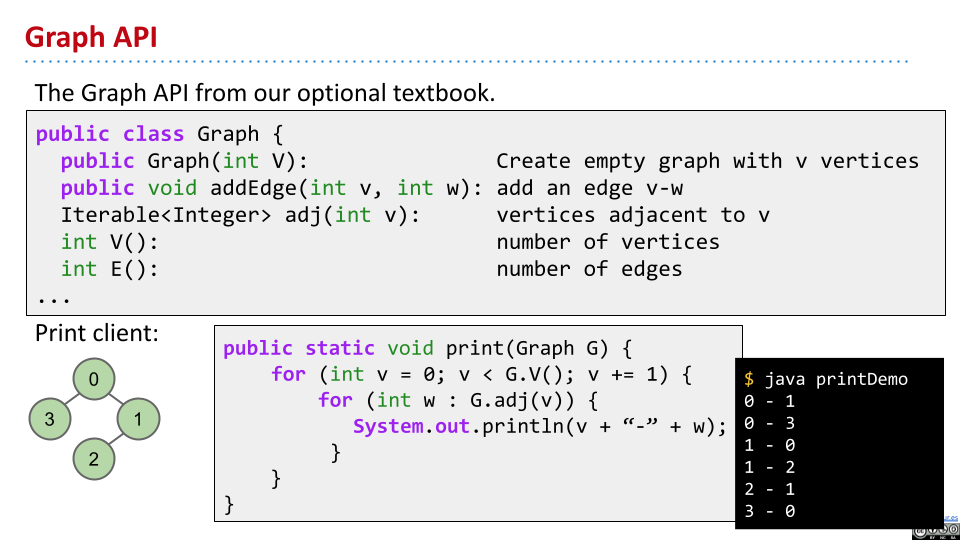
可能有如下的 API。对于这种 API，可以使用遍历的形式，打印出所有的边。 lec21-9.png

图的实现

不同的实现方式会影响运行时间和内存使用量。

1 矩阵

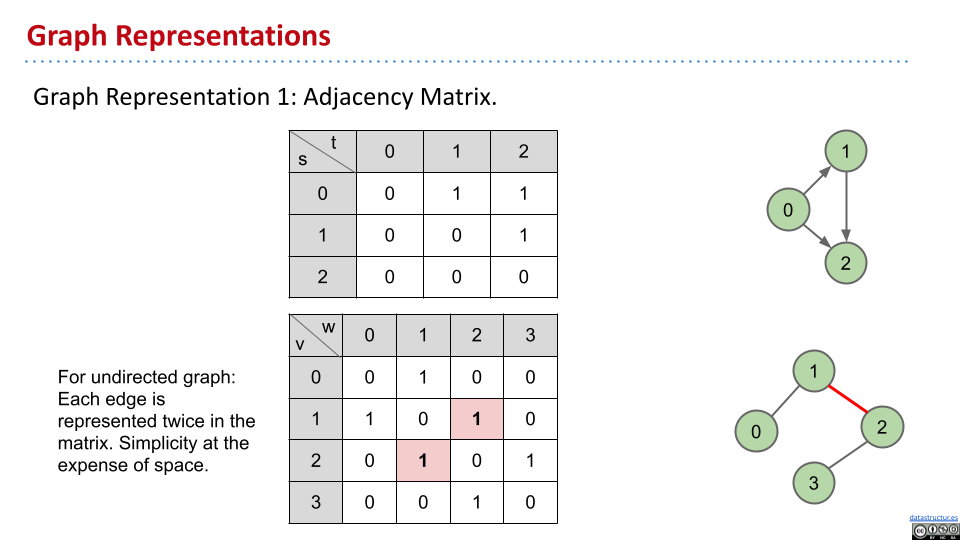
对于有向图，矩阵不是对称的。不过，对于无向图，转置后与原先相同，具有对称性。 lec21-10.png

对于遍历邻居的操作，需要消耗 $\Theta(V)$ 的时间，其中 V 为节点的数量。

2 HashSet

使用 HashSet，Set 中每个元素为 Edge，包含一对节点。

3 列表的数组

数组的索引就是对应节点的值。每个数组中指向一个列表。其中遍历一个节点邻居的运行时间介于 1 到 V 之间。如果要打印所有的边，那么运行时间是 $\Theta(V+E)$，也就是节点和边的个数之和。

对于不同种类的图，因为 V 和 E 之间的数量关系不同，所以打印的运行时间也会不同。

性能比较

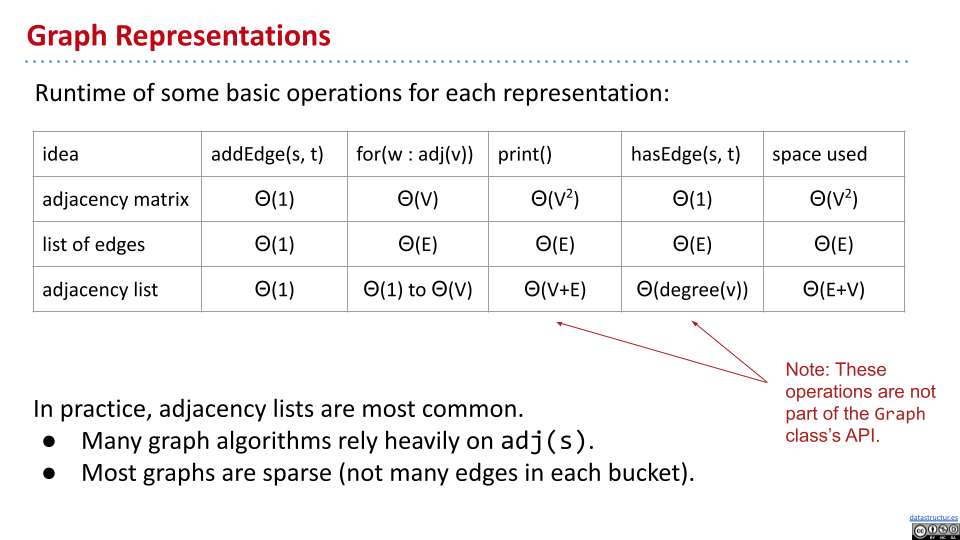lec21-11.png 实际上很多算法依赖于 adj()，而 adjacency list 在这方面的表现最好。

遍历算法和耗时

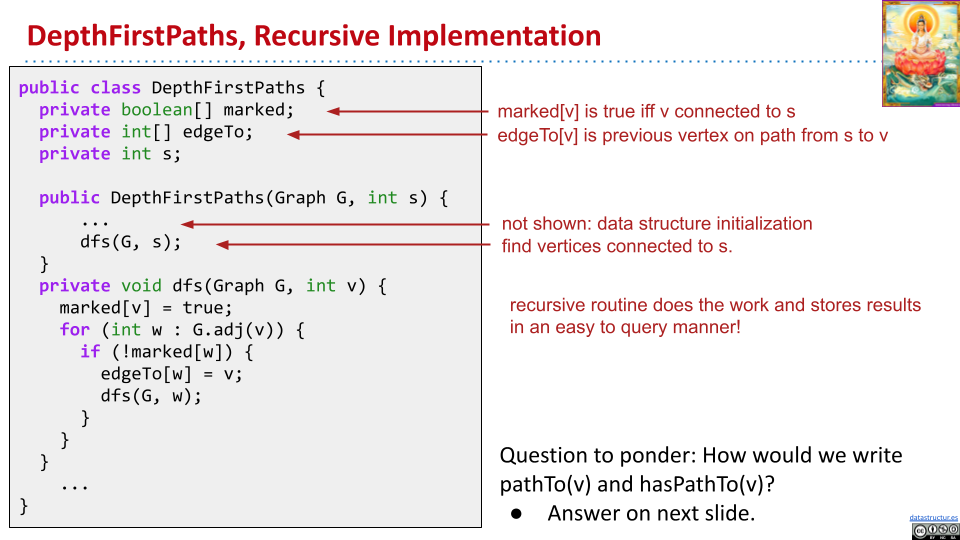
通常将遍历的方法写在另一个类当中，方便使用。 lec21-12.png

只需要使用 marked，就可以判断是否有路径。对于 pathTo 方法，首先需要遍历 edgeTo，然后将储存的路径反向。 lec21-13.png

广度优先的运行时间也是 $O(V+E)$。

lab8 MyHashMap

抽象

首先，需要实现 MyHashMap 继承自接口 Map 61 B，与 lab 7 中一样，都需要拥有一些方法。其中，remove 方法是选做的。

对于 HashTable 而言，具体的 buckets 可以有很多种实现方法，例如链表、数组、二叉树、PQ 等等。为了兼容各样的实现方式，需要使用抽象。

将具体的 Mapping 设置为 Node 类，仅仅包含 key 和 value。上述提到的实现方式都是 Collection，因此，在 MyHashMap 中会有 Collection<Node> createBucket() 方法，返回一个 bucket。例如，通过 return new LinkedList<>();，就可以指定使用链表来实现。

对于其他不同的实现方法，可以继承 MyHashMap，并且 Override 对应的 createBucket() 方法。

对于这当中的 Collection 而言，只应该使用 add、remove 和 iterate 来交互。这样才可以保证不同实现方法的兼容性。

实例变量和初始化

正如说明中所说，为了方便起见，直接使用默认的 HashSet 来创建 key 的集合。

1
2
3
4

private Collection<Node>[] buckets;  
private int size = 0;  
private Set<K> keySet = new HashSet<>();  
private double loadFactor = 0.75;

初始化很简单。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

/** Constructors */  
public MyHashMap() {  
    buckets = createTable(INIT_SIZE);  
}  
  
public MyHashMap(int initialSize) {  
    buckets = createTable(initialSize);  
}

public MyHashMap(int initialSize, double maxLoad) {  
    buckets = createTable(initialSize);  
    loadFactor = maxLoad;  
}

为了保持一致性，使用 createNode 和 createTable 方法。特别注意，createTable 需要调用 createBucket() 方法，这样才能实现多态。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

protected Collection<Node> createBucket() {  
    return new LinkedList<>();  
}

private Collection<Node>[] createTable(int tableSize) {  
     Collection<Node>[] col = new Collection[tableSize];  
     for (int i = 0; i < col.length; i++) {  
         col[i] = createBucket();  
     }  
     return col;  
}

这里还有一个小细节。对于 Collection<Node>[] 的创建，不能写上 <Node>。这是 Java 的小特性，因此直接写 new Collection[tableSize] 即可。

查找

对于清零操作，只需要都赋值为新的空指针就行。

1
2
3
4
5

@Override  
public void clear() {  
    Arrays.fill(buckets, createBucket());  
    size = 0;  
}

为了实现 hashing，需要根据 key 来获取对应的索引。因此，创建 hashIndex 方法。特别注意，当在 resize 的时候，不能简单地使用当前的 buckets 长度来得到索引。因此，这里加入了第二个参数 length。

1
2
3

private int hashIndex(K key, int length) {  
    return Math.floorMod(key.hashCode(), length);  
}

于是，可以实现是否含有 key 的查找方法 containsKey。注意要使用 .equals() 方法。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

@Override  
public boolean containsKey(K key) {  
    Collection<Node> bucket= buckets[hashIndex(key, buckets.length)];  
    for (Node node : bucket) {  
        if (node.key.equals(key)) {  
            return true;  
        }  
    }  
    return false;  
}

对于 get() 方法，几乎一样，只需要返回对应的 value 就可以。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

@Override  
public V get(K key) {  
    Collection<Node> bucket= buckets[hashIndex(key, buckets.length)];  
    for (Node node : bucket) {  
        if (node.key.equals(key)) {  
            return node.value;  
        }  
    }  
    return null;  
}

插入

在插入的时候，有可能会需要调整大小。因此，编写 checkResize() 方法检查是否需要更新大小。

1
2
3
4
5

private void checkResize() {  
    if ((double) size / buckets.length >= loadFactor) {  
        resize(buckets.length * 2);  
    }  
}

在调整大小的时候，需要先创建新的大小的 newbuckets。然后遍历原先 buckets，并且遍历每一个节点。然后，将每一个节点计算 hash 值，放入新的 newbuckets 中。最后让 buckets 指向 newbuckets。注意这里的 hashIndex 在调用时，要使用 newSize。

1
2
3
4
5
6
7
8
9

private void resize(int newSize) {  
    Collection<Node>[] newBuckets = createTable(newSize);  
    for (Collection<Node> bucket : buckets) {  
        for (Node node : bucket) {  
            newBuckets[hashIndex(node.key, newSize)].add(node);  
        }  
    }  
    buckets = newBuckets;  
}

在此基础上，可以实现 put。需要注意，如果之前已经有相同的 key，那么就将原先的 value 替换为新的 value。因此这需要遍历 bucket 中的每一个 node。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

@Override  
public void put(K key, V value) {  
    Collection<Node> bucket= buckets[hashIndex(key, buckets.length)];  
    keySet.add(key);  
    boolean flag = false;  
    for (Node node : bucket) {  
        if (node.key.equals(key)) {  
            node.value = value;  
            flag = true;  
        }  
    }  
    if (!flag) {  
        Node newNode = createNode(key, value);  
        bucket.add(newNode);  
        size += 1;  
    }  
    checkResize();  
}

删除

对于删除操作，只需要遍历相应的 bucket。如果发现有相同值的节点，删除就行。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

@Override  
public V remove(K key) {  
    Collection<Node> bucket = buckets[hashIndex(key, buckets.length)];  
    for (Node node : bucket) {  
        if (node.key.equals(key)) {  
            bucket.remove(node);  
            return node.value;  
        }  
    }  
    return null;  
}  
  
@Override  
public V remove(K key, V value) {  
    Collection<Node> bucket = buckets[hashIndex(key, buckets.length)];  
    for (Node node : bucket) {  
        if (node.key.equals(key) && node.value.equals(value)) {  
            bucket.remove(node);  
            return node.value;  
        }  
    }  
    return null;  
}
© 2024 Ovid的博客
使用 Hugo 构建
主题 Stack 由 Jimmy 设计