Featured image of post CS61B week7 学习笔记
CS

CS61B week7 学习笔记

包括第七周讲座内容和lab7

lec17 B-Trees(2-3, 2-3-4 Trees)

二叉搜索树

Bushy vs. Spindly

对于茂盛的二叉搜索树，高度是 $\Theta(\log(n))$ ；而对于细长的二叉搜索树，高度是 $\Theta(n)$，这时候其实退化成了链表。

判断

哪一个提供了更多信息？

  • 最差情况的 BST 高度为 $\Theta(n)$
  • BST 高度为 $O(n)$

事实上，说最差情况的 BST 高度为 $\Theta(n)$ 提供了更多信息。因为，大 O 不能说明复杂度会达到那个程度，只能说明小于等于。所以，信息量更少。

举例来说，你也可以说二叉搜索树的高度为 $O(n^2)$。现实当中，人们通常默认大 O 表示了最坏情况。

高度、深度与表现

  • Depth：某个节点举例根节点的距离。例如，根节点深度为 0，根节点的子节点为 1。
  • Height：节点深度的最大值。
  • Average depth：节点深度的平均值。如图。

lec17-1.png 高度决定了树在最差情况下的时间，平均深度决定了平均情况下的时间。

随机的树

如果加入物品的顺序不一样，那么树的高度和平均深度可能不一样，表现也就不一样。

不过，如果随机加入元素，可以证明平均深度约为 $2\ln(n)$，树的高度约为 $4.311\ln(n)$。如果包括删除操作，也可以证明随机的树的性能仍然是 $\Theta(\log(n))$。

然而，如果插入的物品是有序的，那么很可能导致较差的情况。例如，储存有序日期的时候，数据总是有序的，这时候普通二叉搜索树的表现较差。

B-Trees 2-3 trees 2-3-4 trees

概念

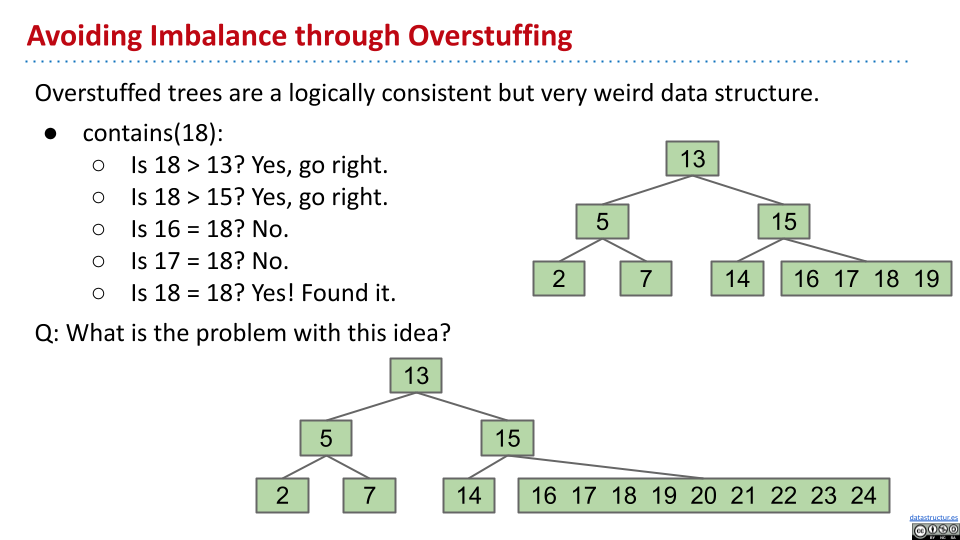
为了不增加新的深度，可以考虑将新的节点插入到原先节点。然而，如果插入得过多，显然会降低性能。 lec17-2.png

可以设置一个限制，如果某个节点多于限制 L，将某个值给父节点。不过，这样有可能失去搜索树的性质。因此，需要增加子节点的数量。

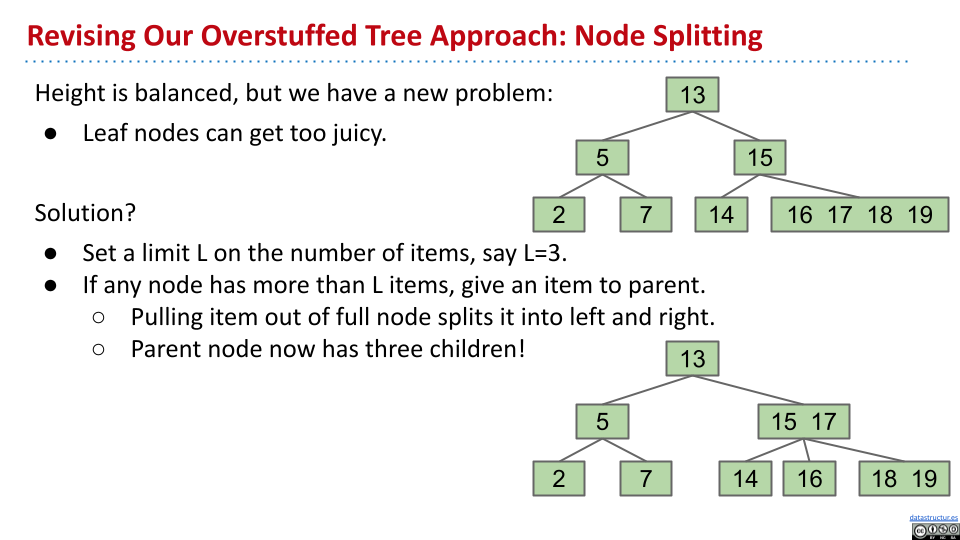lec17-3.png 如果大于 3 个元素，就分割。这个例子中，节点 16 17 18 19 超过了限制，可以让 17 上溢，与 15 融合。中间的 16 分割后介于 15 和 17 之间，是 15 17 节点的第二个子节点。

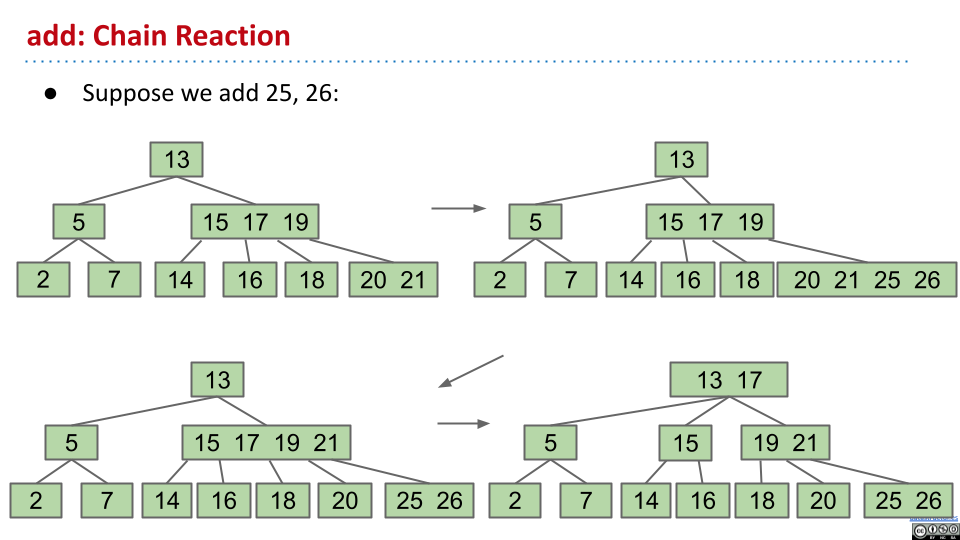lec17-4.png 途中，因为 15 17 19 21 节点的元素个数超过了 3，因此将 17 上升，并分割出 15。

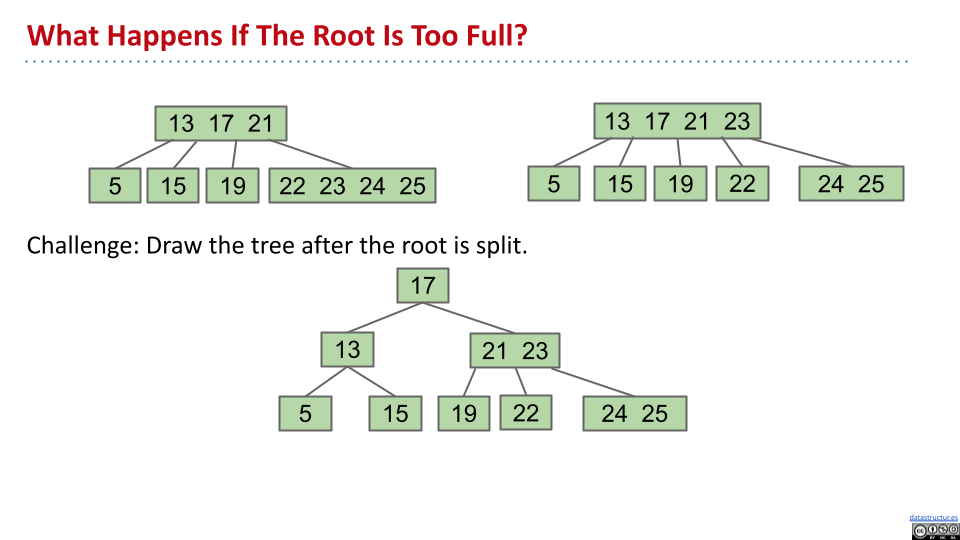lec17-5.png 在这个例子当中，根节点也需要上溢。因此，新的根节点变成了 17，同时将 13 和剩下的节点分开。因此，当根节点充满元素的时候，刚好会提升一层高度，树还是充满的。

分类

如果让 $L=3$，就像上面的示例，那么也称为 2-3-4 树（aka 2-4 树）。这意味着每个节点可能有 2、3、4 个子节点。

如果让 $L=2$，那么也称为 2-3 树，因为可能有 2 个或 3 个子节点。

B 树通常的应用方式有两种：

  • 很小的 L，例如 2 或 3。是简单的平衡搜索树。
  • 很大的 L，例如上千。在实践中用在数据库或者文件管理系统中。

证明

可以证明，无论是怎样的顺序，总可以得到 bushy 的树。

根据 B 树的构造方式，有两个不变量：

  • 所有叶节点具有相同的高度
  • 一个拥有 k 个物品的非叶节点，肯定有 k+1 个子节点

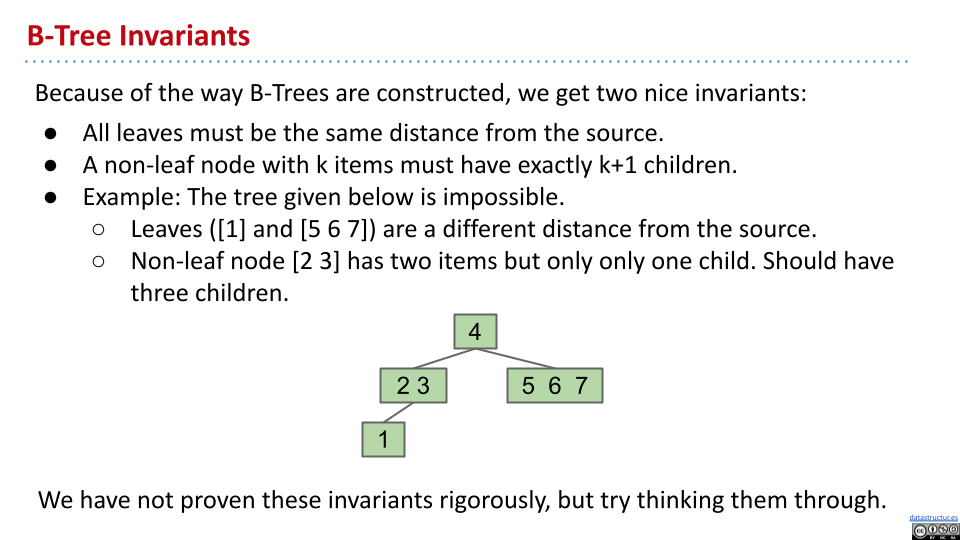lec17-6.png 图中的例子同时违反了这两个不变量。

性能

对于 L 为 2 的 B 树，在最差情况下，高度是 $\log_2(n)$。在最好情况下，高度为 $\log_3(n)$。所以，高度是 $\Theta(\log(n))$。

对于查找操作，设高度为 H。在最差情况下，需要查找 H+1 个节点，同时每次需要遍历 L 个元素。因此时间为 $O(HL)=O(L \log(n))=O(\log(n))$。

可以证明加入操作和删除操作也是 $O(\log(n))$。

lec18 Red Black Trees

树旋转

理解

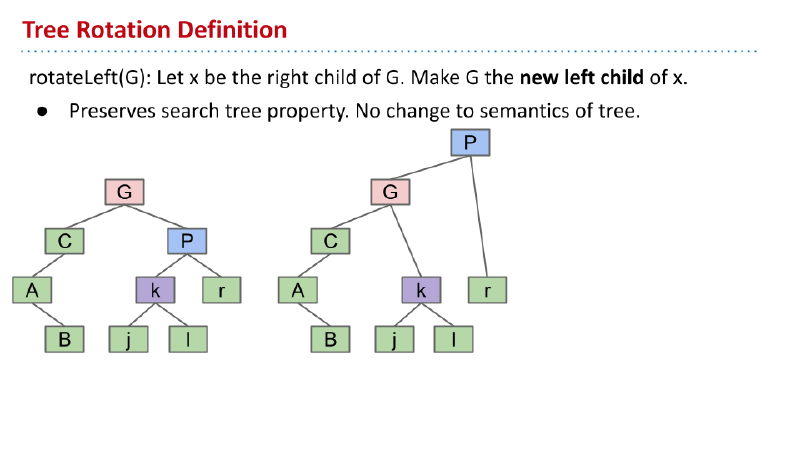
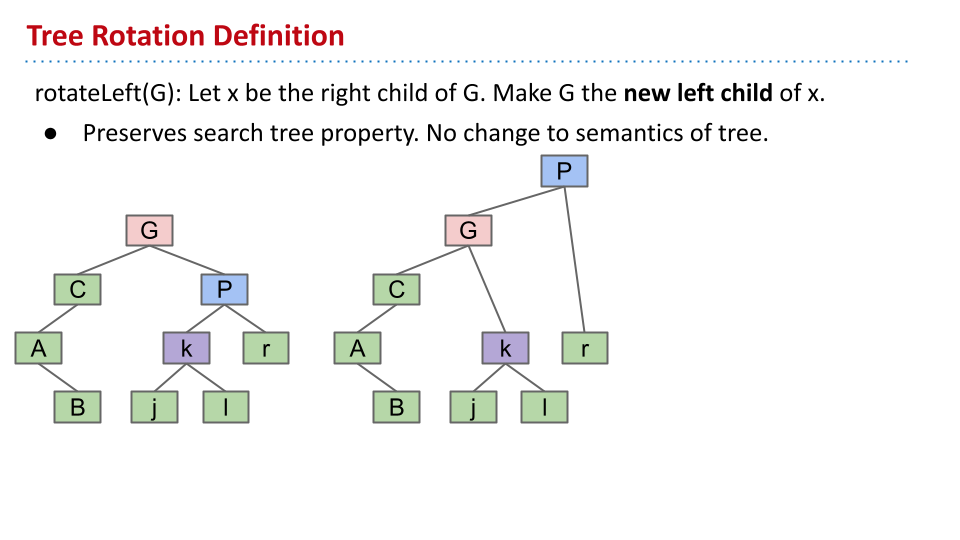
如果要将 G 向左旋转，那么首先让 P 成为 G 的父节点。此时，P 有三个子节点，不符合。因此，让原先 P 的左子节点 k 成为 G 的右子节点。这样就完成了旋转。 lec18-1.png

某节点左旋转：设该节点原先的右节点为 x。则旋转后让 x 的左子节点变成该节点。

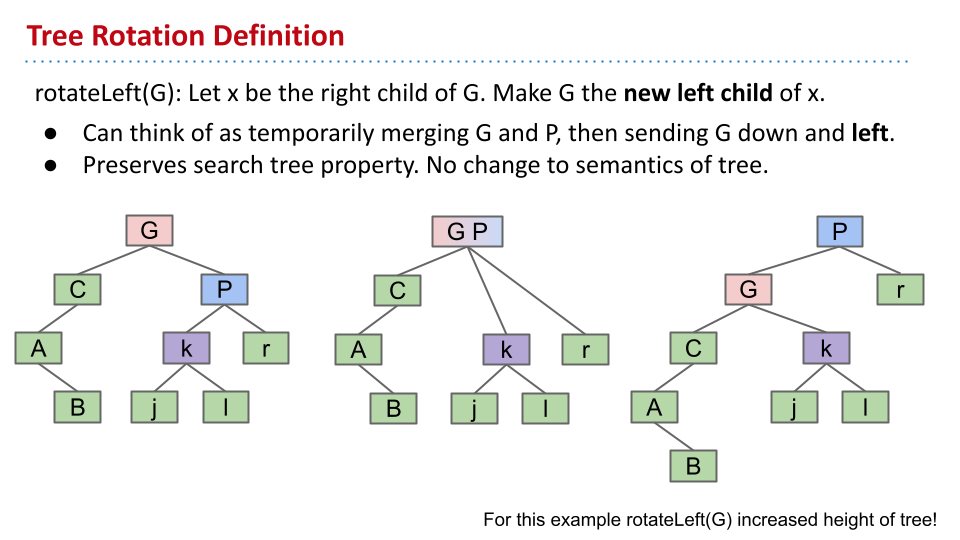
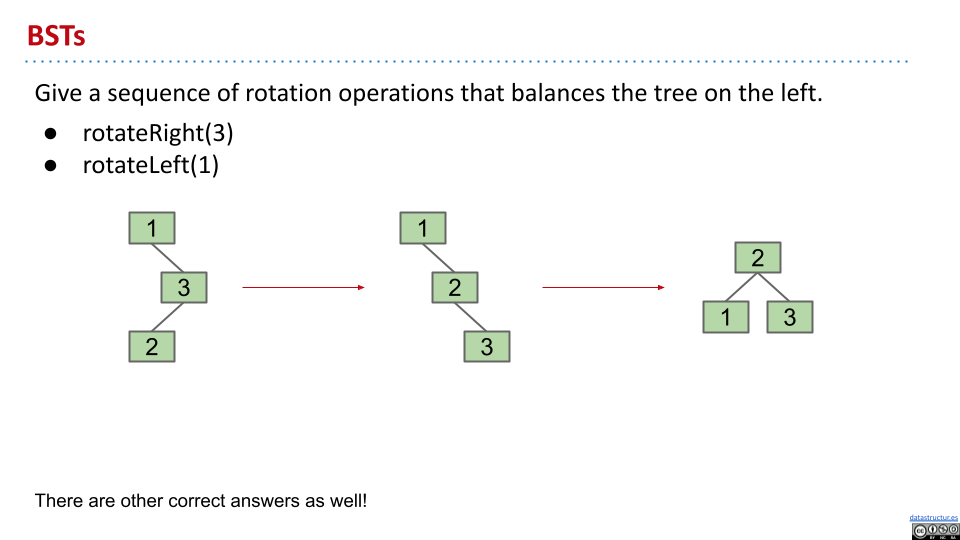
旋转还有另一种理解方法：首先让 P 向上与 G 融合。然后将 G 分裂下来，拥有 C 和 k 两个子节点。 lec18-2.png lec18-3.png

作用

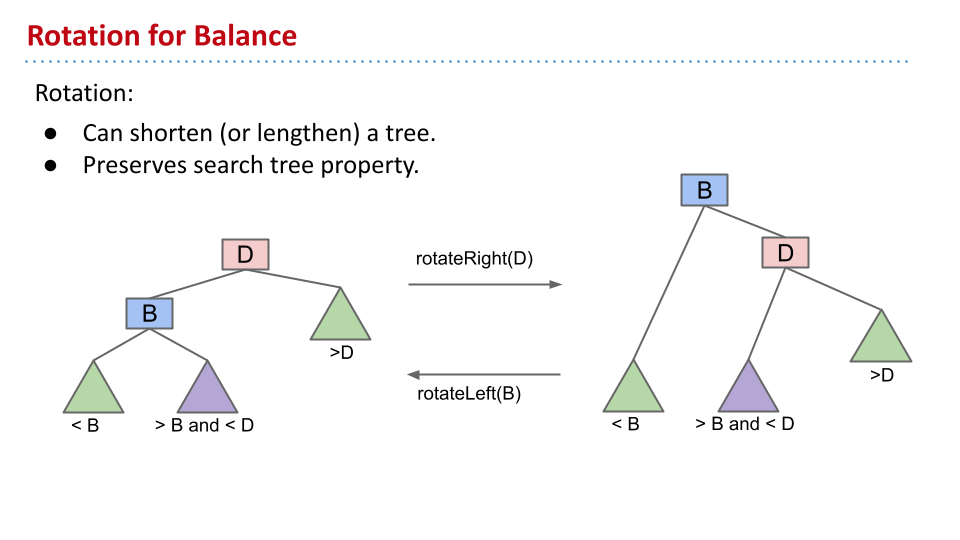lec18-4.png 通过旋转，可以改变树的结构，并缩短高度。理论上来说，利用旋转来平衡一个不平衡的树需要 $O(n)$ 的时间。

红黑树

可以考虑构造和 2-3 树等价的二叉搜索树。

对于只有 2 节点的 2-3 树，每个节点只有一个元素，显然就是 BST。如果有 3 节点，那么就有些麻烦。

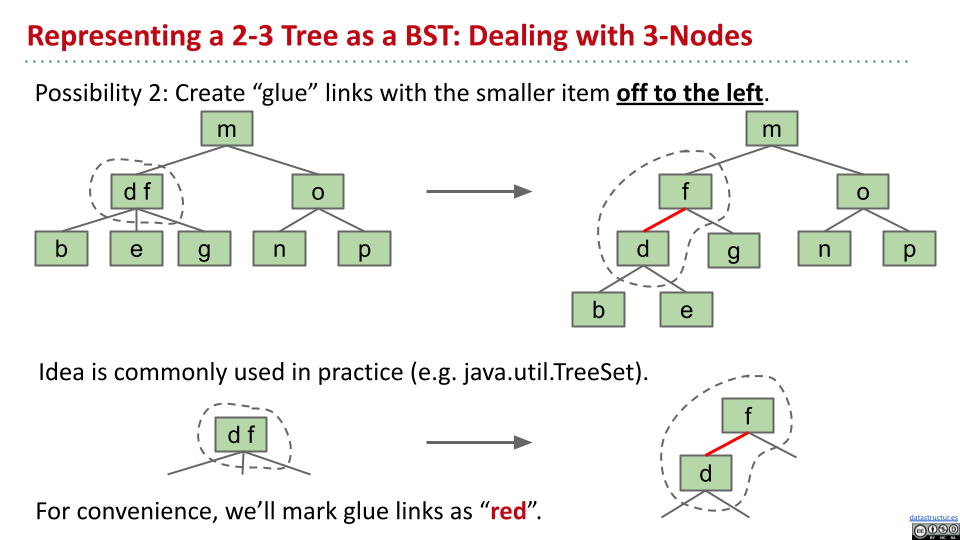lec18-5.png 可以使用“胶水”链接，就较小的元素放在左侧。

概念

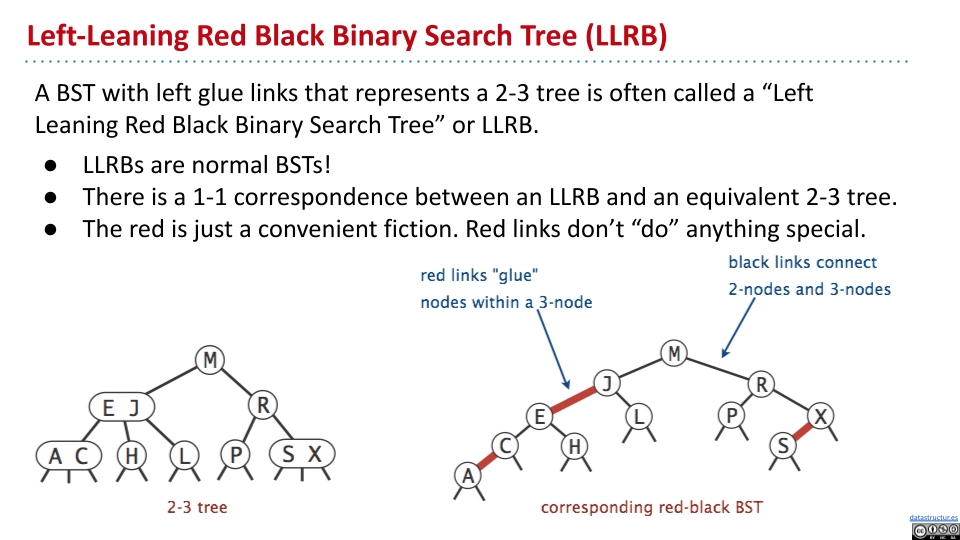lec18-6.png 2-3 树与左倾红黑树有一一对应关系，同时 LLRB 也就是普通的 BST。其中，红色的链接并没有做什么特殊的事。

LLRB 的查找与一般的 BST 一样。

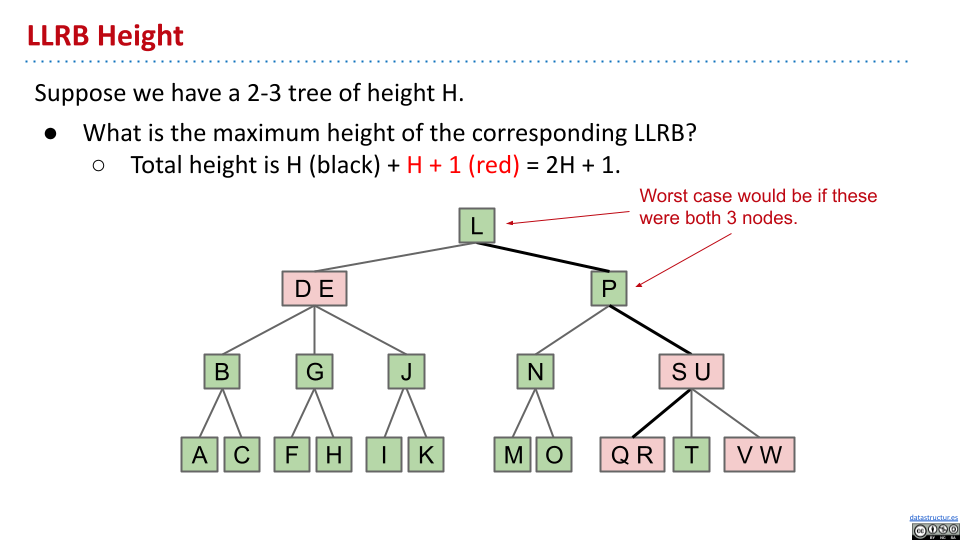lec18-7.png 在几乎都是 3 节点的情况下，设2-3 树的高度为 $H$，则对应的 LLRB 树的高度为 $H+H+1=2H+1$。

性质

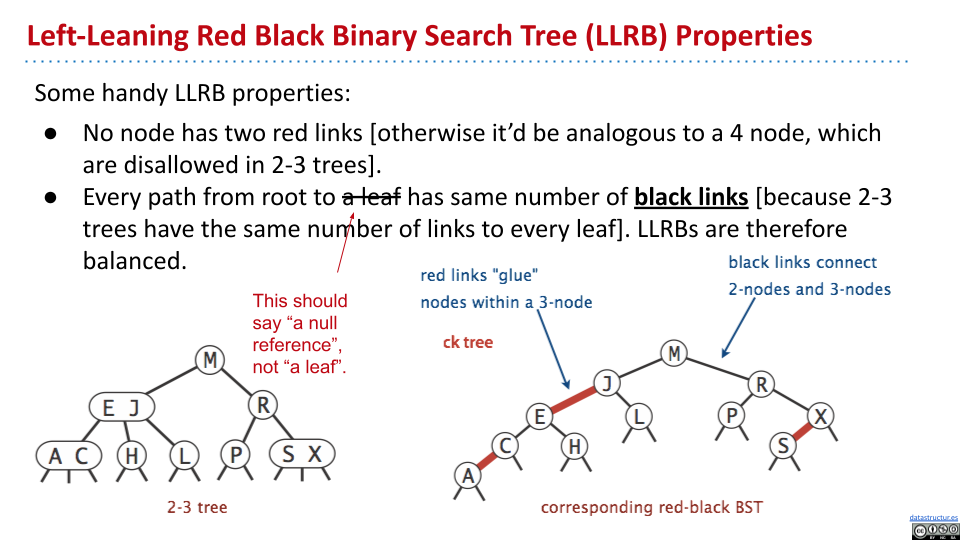
在 2-3 树中，所有叶节点与根节点的距离相同。因此，在对应的 LLRB 中，所有叶节点距离根节点的黑色链接数量相同。同时，因为 2-3 树最多只有 3 节点，因此没有一个节点同时拥有两个红色的链接。 lec18-8.png

构造

因为 LLRB 与 2-3 树的对应关系，因此 LLRB 的高度不会超过 2-3 树高度的大约两倍，所以拥有相同的 $\Theta(\log(n))$ 性能。

为了构造 LLRB，可以在插入元素后，通过一些旋转操作，保持 2-3 树与 LLRB 的对应关系。

1

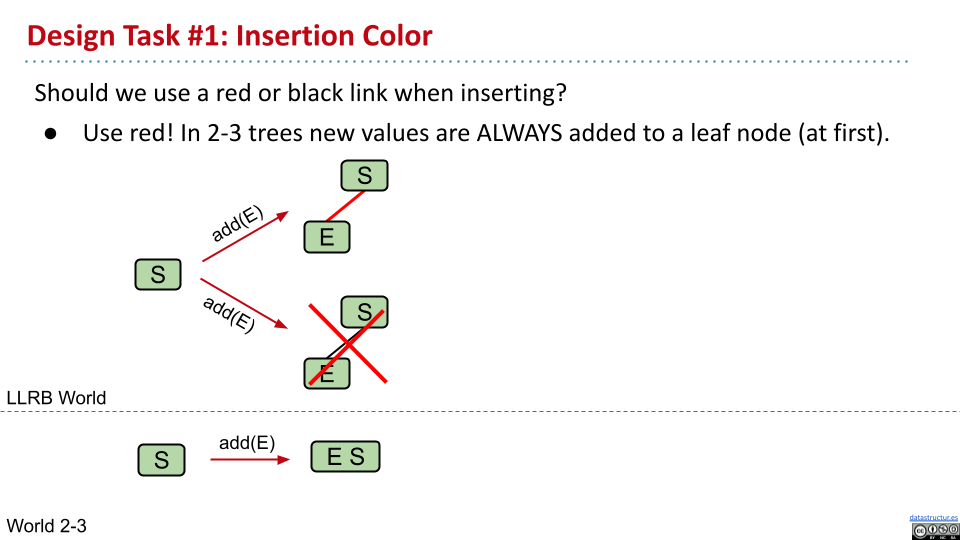
因为在 2-3 树中总是在已有节点上添加元素，因此新加入的节点总是红色链接。 lec18-9.png

2

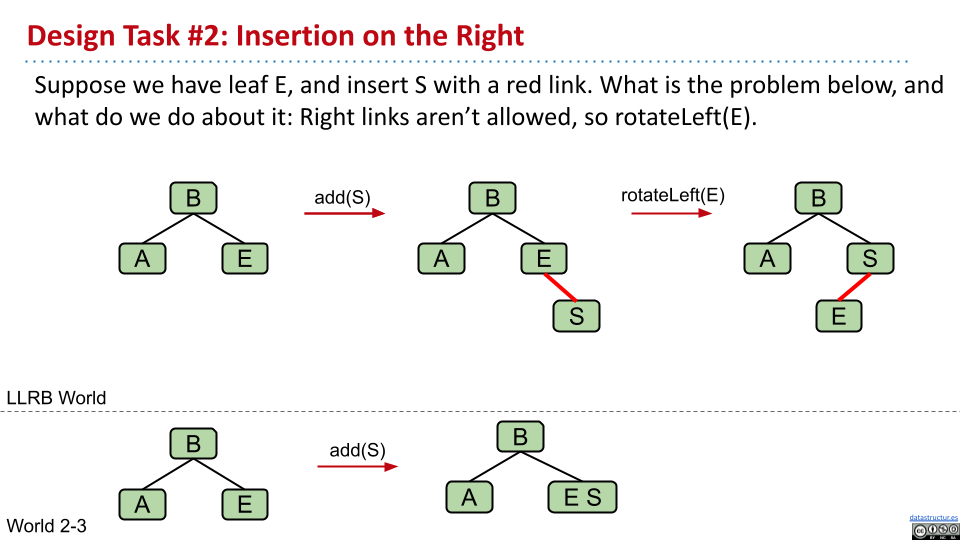
在插入后，如果红色连接方向为右下，那么需要旋转，因为 LLRB 中红色连接总是向左下的。 lec18-10.png

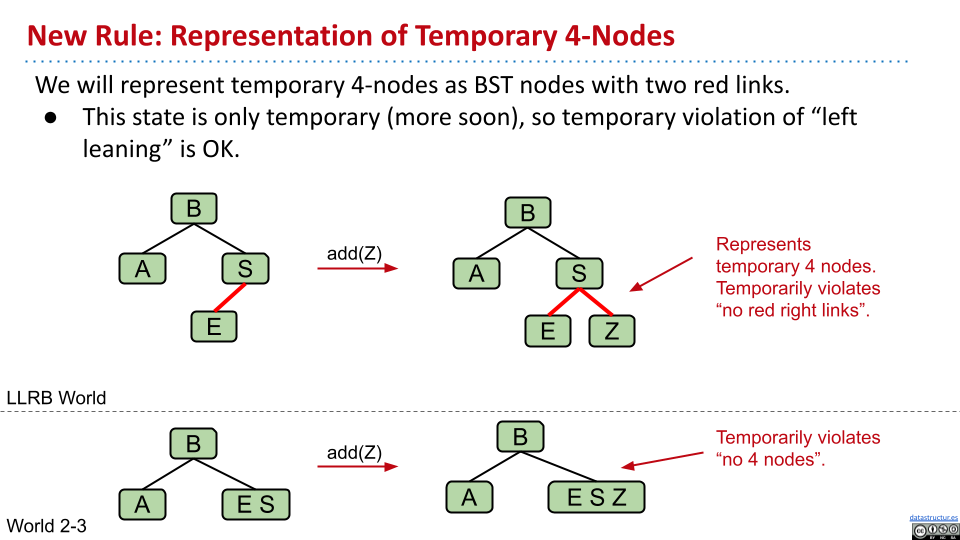
使用两个红色连接，来表示暂时的 4 节点。 lec18-11.png

3

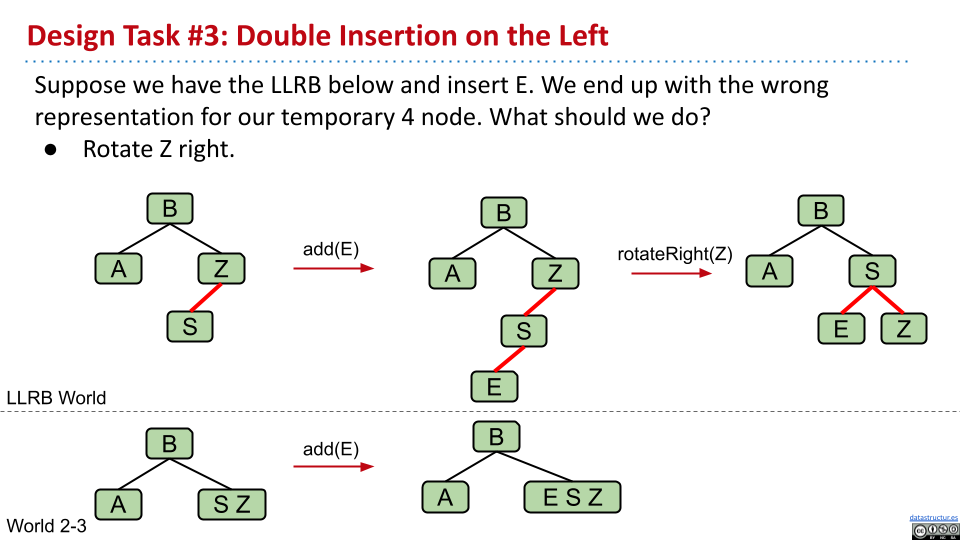
在临时的 4 节点中，如果不符合刚刚的临时节点表示方法，就需要旋转，创造某一个节点的左右子连接为红色。 lec18-12.png

4

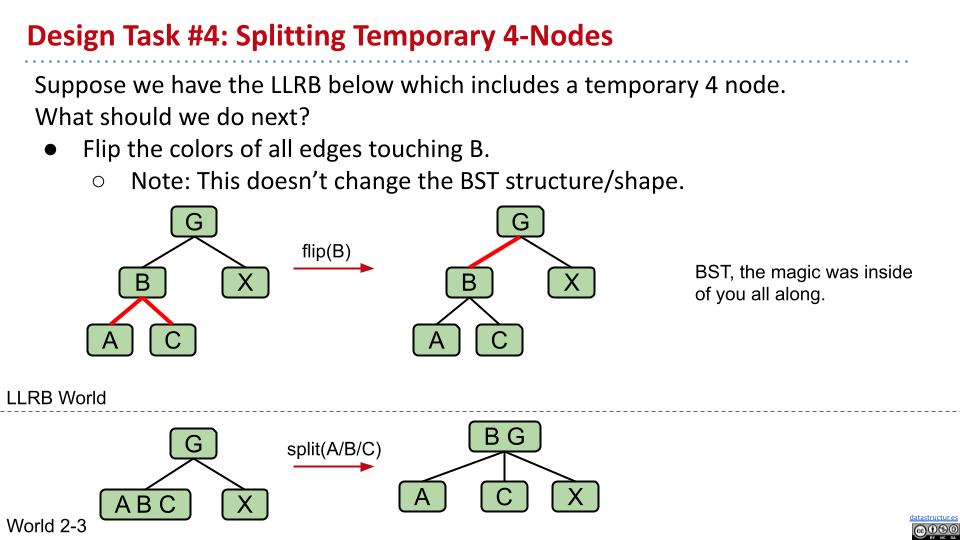
最后，考虑合并。这时候其实并没有涉及到旋转，只需要改变颜色。将所有关于 B 的边的颜色反向。 lec18-13.png

总结，只需要下面三个操作： lec18-14.png

运行时间

插入时间为 $O(\log(n))$。同时，旋转和翻转颜色的操作对于每一次插入，也是 $O(\log(n))$。

（61 B 没有覆盖 LLRB 的删除，不过可以参考 B 树的删除）

搜索树总结

  • BST 简单，但是可能不平衡
  • 2-3 树（B 树）是平衡的，但较难实现并且相对较慢
  • LLRB 的插入较容易实现，删除较难
    • 通过维持与 2-3 树的一对一关系实现
  • Java 的 TreeMap 是红黑树
    • 维持与 2-3-4 树的联系（不是一对一）
    • 允许两侧的辅助链接
    • 实现起来更加复杂，但是明显更快

lec19 hashing

要使用搜索树，元素必须是可比较的，有什么方法不需要比较呢？同时，有没有可能比 $\Theta(\log(n))$ 更快呢？

可以将数据值（整数）作为索引，创造一个 bool 的数组。真就代表有这个数据，否就代表没有。这样的结构拥有 $\Theta(1)$ 的 contains(x) 和 add(x) 速度。然而，缺陷也相当明显，浪费了大量的内存，并且无法表示非正整数。

储存单词

为了存储单词，有一个不聪明的方法，那就是使用第一个字母对应 1 到 26。然而，这样很可能会碰撞，也无法储存数字。

避免碰撞

使用每一位字母乘以 27 的对应次方。例如，“cat"计算可以得出 $$3\times 27^{2}+1\times27^{2}+20\times 27^{0} = 2234$$其中，a 代表 1，z 代表26。

对于纯英文单词，只要选择的基数大于等于 26，就不会发生碰撞。

编码

从 33 到 126 的 ASCII 码是可以打印的。 同样，在 ASCII 之外，Unicode 也是支持的。可以用这个方法来 hash 中文。

整数上溢

在 Java 中，最大的整数为 2147483647。超过这个数的正数会上溢。这会带来碰撞。

Java 中 int 的最多元素为 4294967296。如果元素超过这个值，就肯定有碰撞，也就是抽屉原理。

有两个问题：

  • 如何处理碰撞？
  • 如何计算任意物品的哈希码？

解决碰撞

可以让 hash 数组的元素表示指针，指向链表。每个链表当中可以有许多物品。

最差情况时间 Contain Insert
Bushy BSTs $\Theta(\log(n))$ $\Theta(\log(n))$
数据索引数组 $\Theta(1)$ $\Theta(1)$
索引数组链表 $\Theta(Q)$ $\Theta(Q)$

其中，Q 是最长链表的长度。HashCode 可以利用取余数，得到某一区间内的整数。

优化

假设数组的大小是固定的 M，则当 N 不断增大超过 M 后，Q 就与 N 成正比，最终的时间就变成了 $\Theta(n)$，性能不好。

因此，考虑让 M 的大小不断增大，这和 project1 中的 ArrayDeque 类似。如果 N/M 大于某一个数，例如 1.5，那么就让 M 的大小翻倍。

每一次扩大 M 需要消耗 $\Theta(n)$ 的时间，但是之后每一次操作只需要消耗 $\Theta(1)$ 的时间，因此整体的时间复杂度还是 $\Theta(1)$。

Java 中的 hash

Java 中所有对象都必须实现 .hashCode() 方法。默认的方法会返回该对象的内存地址。

Java 中的 % 对于负数的处理不满足我们的预期，可能得到负数，而不是正数。因此，使用 Math.floorMod(x, mod)。

警告：

  • 不要使用 HashSet 或 HashMap 来储存会改变状态的对象
  • 在 override equals 的时候也需要 override hashCode，不然会引发诡异的现象

Java 中 String 实际上使用的指数为 31，而不是 126 这样较大的数。这是因为计算的上溢，导致 126^32=126^33=...=0，所以如果使用 126 作为基数，无法区分长度大于 32 的字符串。

lab7

这个 lab 需要使用二叉搜索树来实现 Map，即 BSTMap。其中，只用实现一些相对简单的方法。而一些复杂的方法，例如 remove、iterator 和 keySet 则是选做。

泛型处理

如果希望指定某一个泛型继承自某一个类，需要使用 bounded type parameter，例如下面的代码：

1
2
3
4
5
6
7
8

public class NaturalNumber<T extends Integer> {
	private T n;
	public NaturalNumber(T n)  { this.n = n; }
	public boolean isEven() {
		return n.intValue() % 2 == 0;
	}
	// ...
}

因此，一开始的类就需要写好：

1
2

public class BSTMap<K extends Comparable<K>, V> implements Map61B<K, V> {
}

这是为了保证 key 的类型 K 是可以比较的，因此可以使用 compareTo 方法。

实现

为了实现 BSTMap，首先可以定义内部的节点 Node，方便使用递归。显然，每一个节点需要有 key，value，以及左右指针。

1
2
3
4
5
6

private class Node<K, V> {  
    K key;  
    V value;  
    Node<K, V> left;  
    Node<K, V> right;
}

在实例变量中，储存根节点和 size。

1
2

Node<K, V> root;  
int size = 0;

这样，clear() 方法清除该树，size() 方法返回大小，都很容易实现。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

@Override  
public void clear() {  
    root = null;  
    size = 0;  
}  
  
@Override  
public int size() {  
    return size;  
}

搜索

为了实现 BST 的搜索功能，首先定义一个帮助函数 searchKey。如果当前节点为空，则返回 null；如果当前节点的值与 key 相同，则返回当前节点；如果要搜索的 key 小于当前值，则在左侧树种查找；否则在右侧树查找。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

/** Helper method to recursively search key. */  
private Node<K, V> searchKey(Node<K, V> now, K key) {  
    if (now == null) {  
        return null;  
    }  
    if (key.equals(now.key)) {  
        return now;  
    }  
    if (key.compareTo(now.key) < 0) {  
        return searchKey(now.left, key);  
    }  
    return searchKey(now.right, key);  
}

这样，就可以很方便地实现 containsKey(K key) 方法，只用看是否返回值为 null 即可。

1
2
3
4
5
6
7

@Override  
public boolean containsKey(K key) {  
    if (searchKey(root, key) == null) {  
        return false;  
    }  
    return true;  
}

同样地，查找当前 key 对应的 value 也可以实现：

1
2
3
4
5
6
7

@Override  
public V get(K key) {  
    if (searchKey(root, key) == null) {  
        return null;  
    }  
    return searchKey(root, key).value;  
}

插入

为了实现插入功能，构造帮助函数。如果当前节点为 null，就直接返回新的包含 key 和 value 的节点。如果插入的 key 小于当前值，则在左侧插入；如果插入的 key 大于当前值，则在右侧插入。如果相等，则说明 key 已经存在，只需要更改 value 即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

/** Helper method to insert item. */  
private Node<K, V> insert(Node<K, V> now, K key, V value) {  
    if (now == null) {  
        keySet.add(key);  
        return new Node<>(key, value, null, null);  
    }  
    if (key.compareTo(now.key) < 0) {  
        now.left = insert(now.left, key, value);  
    }  
    else if (key.compareTo(now.key) > 0) {  
        now.right = insert(now.right, key, value);  
    }  
    else {  
        now.value = value;  
    }  
    return now;  
}

再次基础上，实现 put 方法：

1
2
3
4
5

@Override  
public void put(K key, V value) {  
    root = insert(root, key, value);  
    size += 1;  
}

删除

终于来到了最麻烦的部分。V remove(K key) 需要根据索引 key 来删除相应的节点，并返回被删除节点对应的 value。

首先，判断能不能真正删除节点。利用之前的 searchKey 方法；如果不能，直接返回 null。

之后，储存相应的 val，然后执行 delete 删除。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

@Override  
public V remove(K key) {  
    Node<K, V> result = searchKey(root, key);  
    if (result == null) {  
        return null;  
    }  
    V val = searchKey(root, key).value;  
    root = delete(root, key);  
    size -= 1;  
    return val;  
}

delete 方法的输入为节点和 key，返回值也是节点。如果当前为空，返回空。然后比较 key 与当前节点的 key。如果不相等，就分别在左右子树查找。

在相等的情况下，需要分类讨论：

  • 如果没有子节点，就直接返回 null。
  • 如果有一个子节点，就返回相应子节点的指针。
  • 如果有两个子节点，需要找到在当前节点左侧的最大节点，然后将值赋给当前节点。之后删除左侧最大节点。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

private Node<K, V> delete(Node<K, V> now, K key) {  
    if (now == null) {  
        return null;  
    }  
    int cmp = key.compareTo(now.key);  
    if (cmp < 0) {  
        now.left = delete(now.left, key);  
    } else if (cmp > 0) {  
        now.right = delete(now.right, key);  
    } else {  
        switch (countChildren(now)) {  
            case 0:  
                return null;  
            case -1:  
                return now.left;  
            case 1:  
                return now.right;  
            case 2:  
                Node<K, V> other = findBiggestLeft(now.left);  
                now.key = other.key;  
                now.value = other.value;  
                now.left = deleteMax(now.left);  
        }  
    }  
    return now;  
}

其中，需要完成三个方法： 一： countChildren 计算当前节点的子节点个数。很简单，这里略过。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

private int countChildren(Node<K, V> now) {  
    if (now.left == null && now.right == null) {  
        return 0;  
    } else if (now.left != null && now.right == null) {  
        return -1;  
    } else if (now.left == null && now.right != null) {  
       return 1;  
    }  
    return 2;  
}

二： findBiggestLeft 找到最大子节点。

1
2
3
4
5
6

private Node<K, V> findBiggestLeft(Node<K, V> now) {  
    if (now.right == null) {  
        return now;  
    }  
    return findBiggestLeft(now.right);  
}

三：deleteMax 删除最大节点。

1
2
3
4
5
6
7

private Node<K, V> deleteMax(Node<K, V> now) {  
    if (now.right == null) {  
        return now.left;  
    }  
    now.right = deleteMax(now.right);  
    return now;  
}

完成了这些函数，就可以实现 BST 的删除功能。

© 2024 Ovid的博客
使用 Hugo 构建
主题 Stack 由 Jimmy 设计