Featured image of post CS61B week6 学习笔记
CS

CS61B week6 学习笔记

包括第六周讲座内容和lab6

lec14 Disjoint Sets

这个数据结构应该有两个操作：

  • connect(x, y) 连接 x 和 y。
  • isConnected(x, y) 判断 x 和 y 是否是连接的。同时，连接可能是间接的。

为了实现这个数据结构，重点考虑不同元素是否在同一组当中。一开始，每个元素都是不同的组。如果将两个连接起来，就会把组连接起来。不用考虑具体的连接。

Idea 1

使用集合的列表。但是这样查找起来会很慢。例如，如果要判断 5 和 6 是否连接，必须遍历列表，消耗时间为 $\Theta(n)$。

实现方法 constructor connect isConnected
ListOfSetsDS $\Theta(n)$ $O(n)$ $O(n)$

Idea 2

使用一个数组，每个索引对应元素，数组中每个相同的值对应同一个组。这些值只要相同就行，不关心具体数值。现在，因为数组读取特定元素只是常数，所以 isConnected 方法为 $O(1)$。然而，connect 方法还是较慢，需要遍历数组。

实现方法 constructor connect isConnected
ListOfSetsDS $\Theta(n)$ $O(n)$ $O(n)$
QuickFindDS $\Theta(n)$ $\Theta(n)$ $\Theta(1)$

Idea 3

数组中，记录每一个节点的父节点。如果值为-1，则代表为父节点。

在改变连接的时候，只需要修改一个节点就可以。但是，如果树很长，要“爬树”，需要消耗较长时间 $O(n)$；同时，最坏情况下，isConnected 也需要消耗 $O(n)$。

实现方法 constructor connect isConnected
ListOfSetsDS $\Theta(n)$ $O(n)$ $O(n)$
QuickFindDS $\Theta(n)$ $\Theta(n)$ $\Theta(1)$
QuickUnionDS $\Theta(n)$ $O(n)$ $O(n)$

Idea 4

总是将较小的树放在较大的树下面，通过重量来选择。同时，负数的绝对值大小代表成员个数。保证较少元素的树合并到较大元素的树。

可以证明，树的高度是 $\Theta(\log(n))$。

实现方法 constructor connect isConnected
ListOfSetsDS $\Theta(n)$ $O(n)$ $O(n)$
QuickFindDS $\Theta(n)$ $\Theta(n)$ $\Theta(1)$
QuickUnionDS $\Theta(n)$ $O(n)$ $O(n)$
WeightedQuickUnionDs $\Theta(n)$ $O(\log(n))$ $O(\log(n))$

Idea 5

在此基础上，如果找到了一些节点的最终根节点，那么就可以把这些节点的 parent 设置为根节点，这样会更快。

最初的操作可能耗时，但最后会相当接近常数。

lec15 Asymptotics II

例子 2 

1
2
3
4
5
6
7

public static void printParty(int n) {
	for (int i = 1; i <= n; i = i * 2) {
		for (int j = 0; j < i; j += 1) {
		System.out.println("hello");
		}
	}
}

一种方法是利用画图，可以夹在两条直线之间。

另一种方法是 $1+2+4+\ldots+N=2N-1$。分析的时候需要注意，这与 $1+2+3+…+Q=\Theta(Q^2)$ 不同。

递归

对于一些递归的问题，如果每次需要调用两次 n-1 的函数，那么复杂度为 $2^N$。

对应公式为 $1+2+4+\ldots+2^{N-1}=2^N-1$。

二分搜索

对于排序好的数组，每次查找中间的元素，根据大小再次左右分。对于最不利的大小为 $N$ 情况，需要消耗 $\log(N)$。因此，时间复杂度为 $O(\log(n))$。

排序

选择排序

涉及到等差数列的求和，复杂度为 $O(n^2)$。

合并数组

对于两个有序数组，将它们合并只需要 $\Theta(n)$。

合并排序

可以把原先的数组分成两个数组，对于两个排序后的数组合并。这样不断二分大小，最终二分的次数是 $\log(n)$。每一层的合并需要 $\Theta(n)$。所以，最后的复杂度为 $\Theta(n\log(n))$。

lec16 ADTs, Sets, Maps, BSTs

抽象数据类型（ADT）

解释

类比 Java，ADT 就好像是接口，不关心具体的实现方式，只要满足 API 就行。因此，对于一种 ADT 可以有多种实现。

不过，不同的实现方式有性能上的差异。例如，对于栈来说，只支持推入和弹出的操作，这时候链表和数组的实现方式带来的复杂度一样（不考虑改变数组大小的话）。

又例如，对于 GrabBag ADT，支持以下操作：

  • insert (int x)：将 x 插入。
  • int remove()：随机从袋子中移除一个物品。
  • int sample()：随机观察袋子中每个物品的值（不删除）
  • int size()：袋子中物品的数量

此时，因为考虑到需要随机读取元素，数组会是更好的实现方式，能带来 $\Theta(1)$ 的性能。

Java 内置 ADT

大多数有用的接口都在 java.util 中。例如，有 List，Set，Map 等等。同时，Java 也提供了许多有用的实现方式。这一节会学习 TreeSet 和 TreeMap。

二叉搜索树（BST）

引入

对于线性表而言，查找一个元素需要消耗 $\Theta(n)$ 的时间。如何提升性能呢？可以考虑让指针指向线性表中间的元素，然后翻转左侧的指针。接着，对于左右剩下的部分，也可以做类似的处理。这样递归下去，就可以形成二叉树。

定义

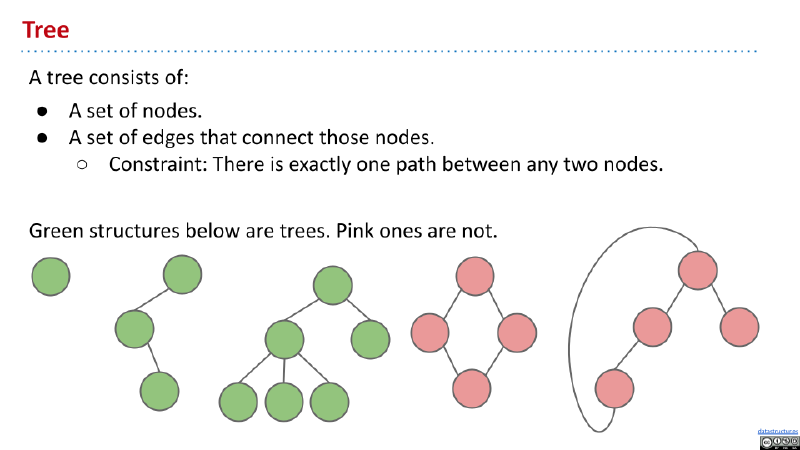
树由以下元素组成：

  • 一些节点的集合。
  • 一些连接节点的边。同时，两个节点之间有且仅有一条路径。

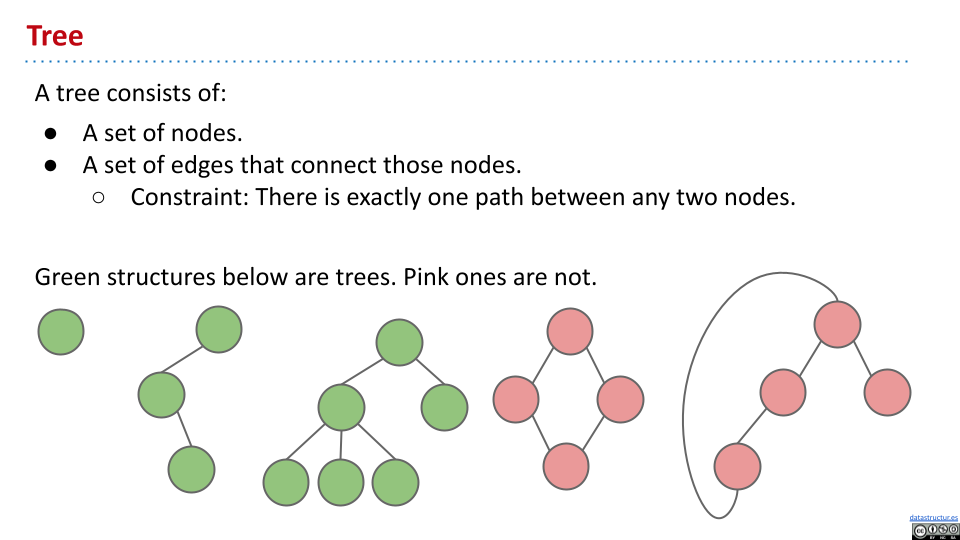
树的示意图

将没有父节点的节点成为根（root），将没有子节点的节点称为叶节点（leaf）。在有根的二叉树中，每个节点拥有 0、1 或 2 个子节点。

对于二叉搜索树来说，对于每个节点，都有以下性质：

  • 左侧子节点的值比当前节点的值小
  • 右侧子节点的值比当前节点的值大

同时，这种排序方式需要是明确的。

搜索

对于二叉搜索树，搜索起来相当简单。如果当前节点的值等于搜索值，就返回。不然，如果搜索值小于当前值，就在左侧子树上搜索；否则在右侧搜索。

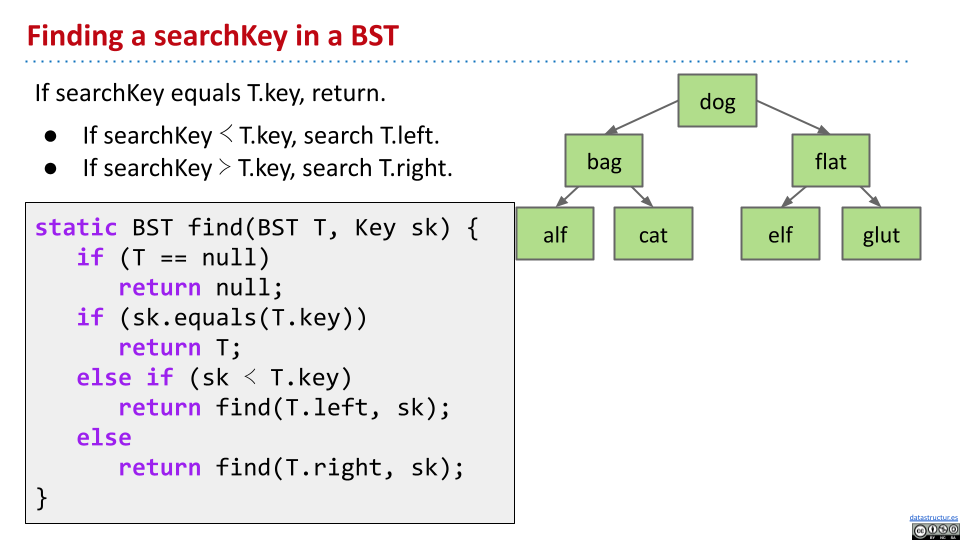
二叉树搜索

可以发现，对于“茂盛”的二叉搜索树，最差情况下搜索只需要 $\Theta(\log(n))$。在实际程序中，这个性能是够用的。

插入

搜索当前的插入值。如果找到了当前值，就返回。否则，就需要创建新节点，并且设置新的指针。

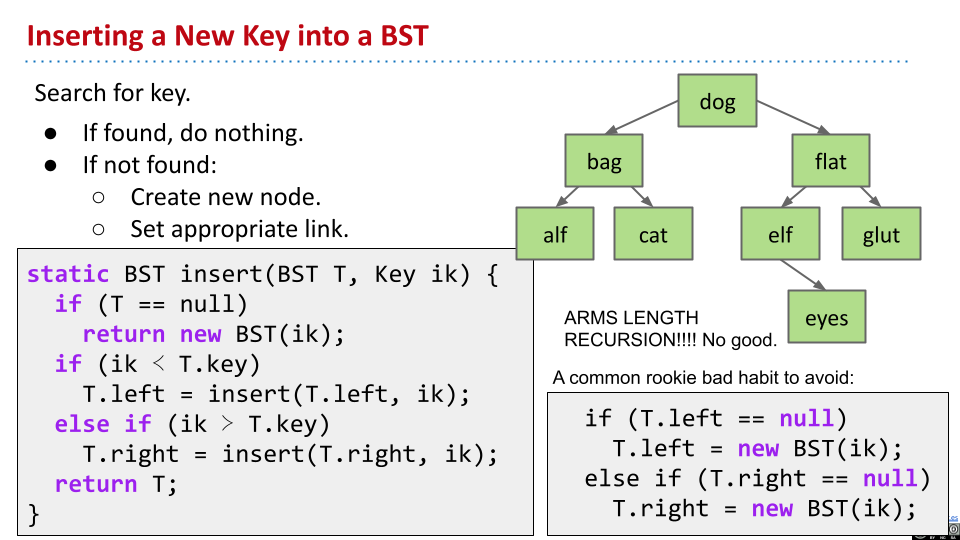
二叉树插入

在上面的事例代码中，需要注意，不要写成右侧的代码。右侧代码并没有真正相信递归，没有处理好 base case，只会增加复杂性。实际上，如果没找到节点，就返回新创建节点的指针；如果找到了，就直接返回 T，也就是不改变当前树。这样才是更高效的做法。

删除

二叉搜索树的删除分为三种情况：

  1. 要删除的节点没有子节点
  2. 要删除的节点有一个子节点
  3. 要删除的节点有两个子节点

对于第一种情况，很明显只需要将父节点的指针删去即可。

对于第二种情况，需要保持二叉搜索树的特性。

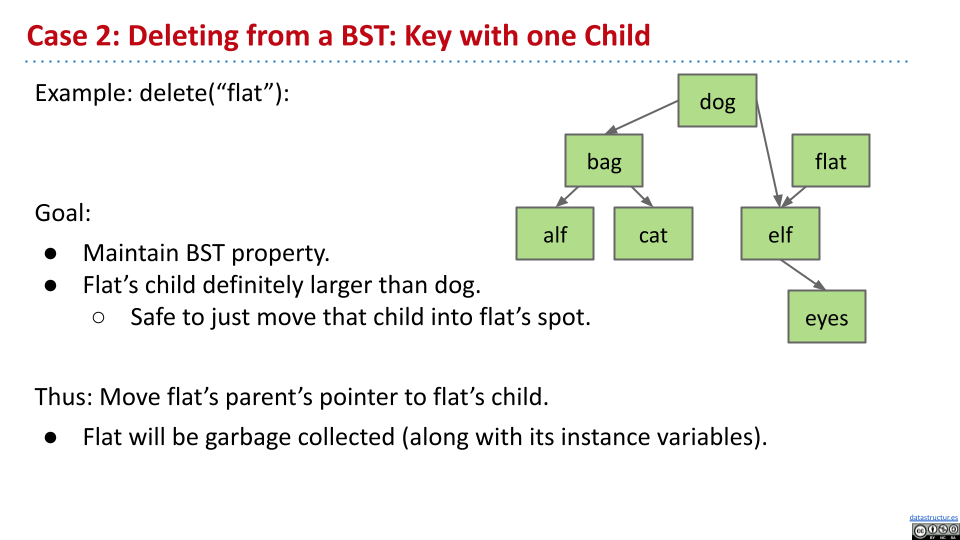
二叉树删除情况二

在这个例子中，为了删去 flat 节点，可以发现 flat 的各个子节点都是大于 flat 的父节点——dog，因此可以直接将 dog 指向 flat 的子节点 elf，满足二叉搜索树的特性。

对于第三种情况，在下图中删除 k 节点。

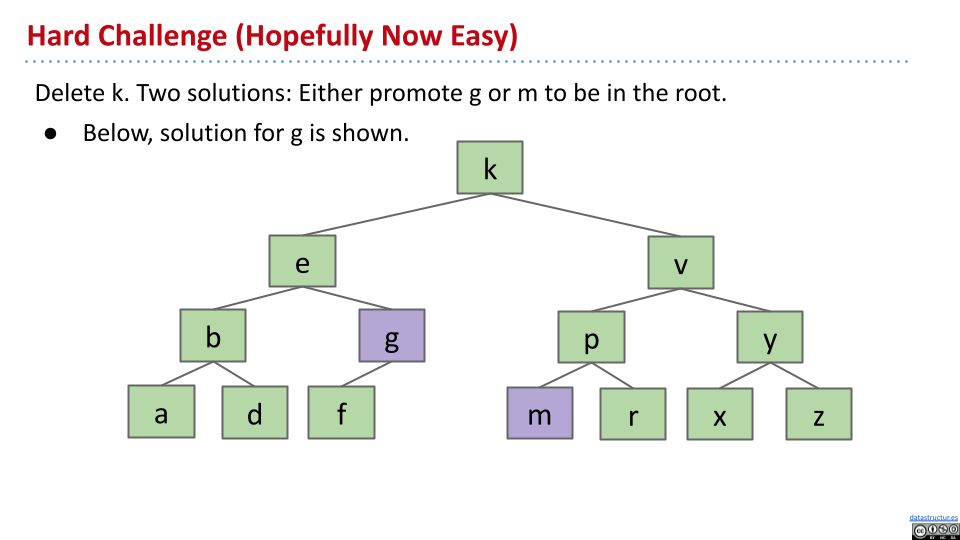
二叉树删除情况三

这时候，为了方便起见，可以考虑保留 k 这个节点，只是更换当中的值。那么，这个新的值必须要比左侧所有节点的值大，比右侧所有节点的值小。

通过观察发现，左子树的最大值 g 和右子树的最小值 m 符合要求，因此可以选取其中之一更换 k 的值。然后，删除 g 或 m。此时，如果要被删除的节点有两个子节点，就不满足上面最小值或最大值的情况，因此该节点只能有 0 个或 1 个子节点，删除它也就变成了前两种情况。

应用

二叉搜索树可以实现集合和字典。因为二叉搜索树没有重复元素，因此满足了集合和字典的要求。

对于集合，只用将元素作为二叉搜索树的值。对于字典，只需要同时储存 key 和 value 即可。

lab6

这一个 lab 主要是为了 project 2 做准备，包括如何使用命令行来使用 Java，如何使用路径，以及如何让程序保存状态。

Java 命令行

一般来说，先要通过 javac 将源代码转换成二进制类文件，然后使用 java 运行程序。同时，利用命令行运行程序时，命令会储存到 main 的 args 中。

Make

通过 makefile，可以方便地编译大型程序。这里也没有细说，只是展示了可以这样，并且提供了 make 来编译程序，使用 make check 来运行本地的测试程序。

Java 路径

使用 System 中的方法 getProperty("user.dir") 来获取当前路径。

1
2
3
4
5
6

// file /home/Michelle/example/Example.java
class Example {
  public static void main(String[] args) {
     System.out.println(System.getProperty("user.dir"));
  }
}

也介绍了绝对路径和相对路径的概念。

Java 文件

使用如下代码来使用文件。

1

File f = new File("dummy.txt");

创建文件：

1

f.createNewFile();

检查文件是否存在：

1

f.exists()

文件夹在 Java 中也是通过 File 来表示的。例如，创建一个文件夹对象：

1

File d = new File("dummy");

创造文件夹：

1

d.mkdir();

序列化 Serializable

在 java.io.Serializable 有相应的接口，需要继承。

1
2
3
4
5

import java.io.Serializable;

public class Model implements Serializable {
    ...
}

然后，写入类文件：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

Model m = ....;
File outFile = new File(saveFileName);
try {
    ObjectOutputStream out =
        new ObjectOutputStream(new FileOutputStream(outFile));
    out.writeObject(m);
    out.close();
} catch (IOException excp) {
    ...
}

会将 m 转化为字节，并存储到文件中。之后，可以读入文件：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

Model m;
File inFile = new File(saveFileName);
try {
    ObjectInputStream inp =
        new ObjectInputStream(new FileInputStream(inFile));
    m = (Model) inp.readObject();
    inp.close();
} catch (IOException | ClassNotFoundException excp) {
    ...
    m = null;
}

使用了帮助函数后，写入和阅读更加简单：

1
2
3
4
5

Model m;
File outFile = new File(saveFileName);

// Serializing the Model object
writeObject(outFile, m);

1
2
3
4
5

Model m;
File inFile = new File(saveFileName);

// Deserializing the Model object
m = readObject(inFile, Model.class);

Exercise

这个练习只需要根据步骤一步步做即可。不过可能是我的终端环境有些问题，怎么改也很难运行 make check。最后只能在 testing/ 文件夹下手动运行 python tester.py --src=our-src .\our\test01-basic-story.in 来测试。

调试

对于拥有持久性的程序，不能简单地像之前那样调试。不过，可以使用 IDEA 的远程 JVM 调试，设置断点，然后利用终端执行命令，使用 s 步入，就可以使用 IDEA 继续调试。

© 2024 Ovid的博客
使用 Hugo 构建
主题 Stack 由 Jimmy 设计