lec35 Radix Sorts
例子
Sleep Sort
对于整数数组,遇到整数 x,就睡觉 x 秒,然后打印出 x。
Counting Sort
对于从 0 开始的连续整数,创造一个新的数组,每次将整数放到相应的索引处。时间复杂度为 $\Theta(n)$。这里没有比较。
让这个想法一般化。首先扫描数组,使用另一个数组来记录元素和对应的个数。然后,计算出每个元素在数组中开始的位置。每次放入一个元素,就更新元素开始的位置。显然,这样的排序会保留原先的顺序,具有稳定性。
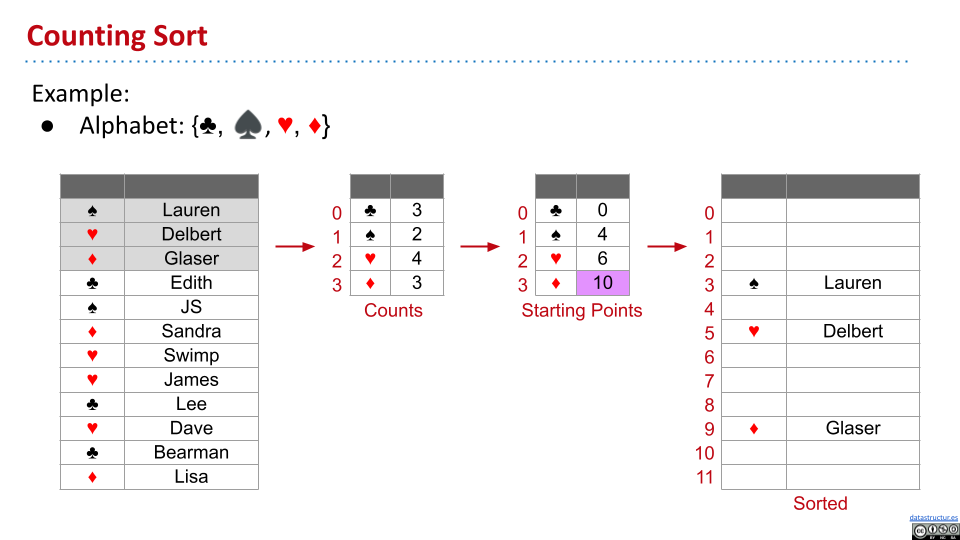
但是,对于很大范围的数据,计数排序会创造空间很大的数组,消耗较多时间。
对于有 N 个 keys,使用 R 个元素的字符表,那么计数排序的耗时为 $\Theta(N+R)$,空间一样。所以当 N 大于 R 时,得到的性能不错。
计数排序只适用于数值有限的数组,不适用于字符串。
LSD Radix Sort
LSD 指的是 Least Significant Digit,也就是最后一位。
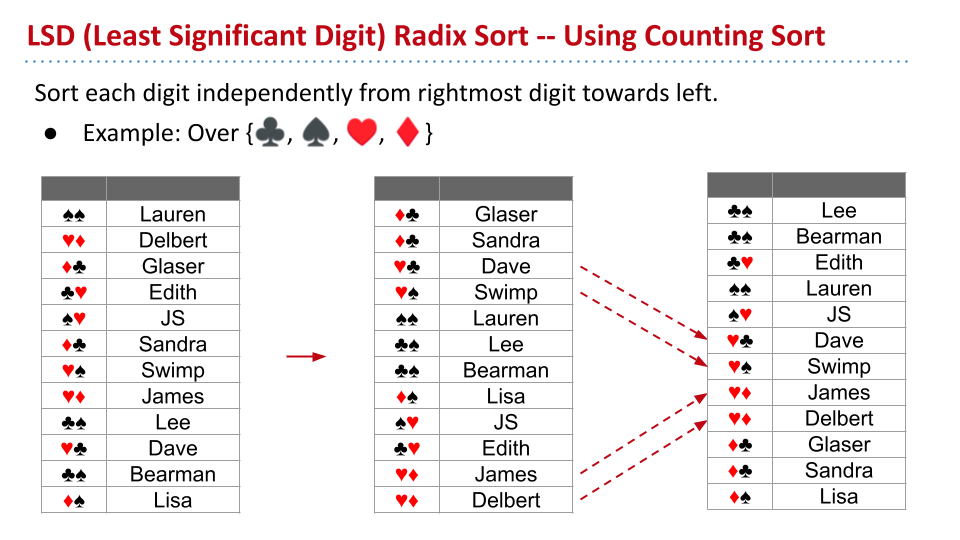
因为计数排序是稳定的,所以第二次排序的时候,末位的顺序是正确的。将花色换成数字也是正确的。
设 W 是位数的长度。那么时间复杂度为 $\Theta(WN+WR)$。当位数不一样时,将前面的位数看成比其他字符更小的字符。
MSD Radix Sort
MSD 代表 Most Significant Digit。对于很长的字符串,从末位开始比较耗时间。直接先比第一个,然后比第二个,会打乱原先顺序。因此,需要分成子问题来处理。
只要分成了首尾,那么只对首位相同的使用第二位的计数排序。如此递归下去。
在最好情况下,只需要看第一位,复杂度为 $\Theta(N+R)$;最坏情况下,需要看每一位,复杂度为 $\Theta(WN+WR)$。然而,和堆排序一样,MSD Sort 对于 caching 也不好。
lec36 Sorting and Data Structures Conclusion
基数排序与归并排序比较
大致理论分析
如果归并排序作用到长度为 W 的字符串上,时间是多少呢?如果每次字符的比较都消耗时间,也就是字符串全都相等,那么最终的耗时就是 $\Theta(WN\log(N))$。
基数排序作用到这个数据上,需要消耗 $\Theta(WN)$ 的时间。理论上来讲,当 N 相当大的时候,并且字符串前面几乎相同时,基数排序更快。
理论计算
通过计算,对于长度 1000 的 1000 个字符串,归并排序的比较次数比 MSD 多了 6 倍多。
实践比较
实践中发现,归并排序比 MSD 快得多,不符合理论。可能是刚刚的模型有问题,只考虑到了比较,没有考虑内存和其他计算。
也有一个很重要的问题:Java 有 Just In Time 编译器。如果某段代码被调用了许多次,编译器会根据它的表现,重新实现代码,大大提高性能。
在这个例子中,经过两次优化后,性能提高了几百倍甚至几万倍。
如果关闭 JIT,那么时间的结果比较吻合理论分析。这告诉我们,算法的执行会受到很多因素的影响,时间复杂度只是其中的一小部分。很多时候只有真正跑起来才能比较性能。
使用基数排序排整数
对于整数,可以使用不同的进制,例如 10、16、256、65336 等等。如果要排列一亿个 int,根据实验,Java 默认的快速排序需要花费 10.9 秒,而基数为 256 的时候表现最好,需要 2.28 秒。
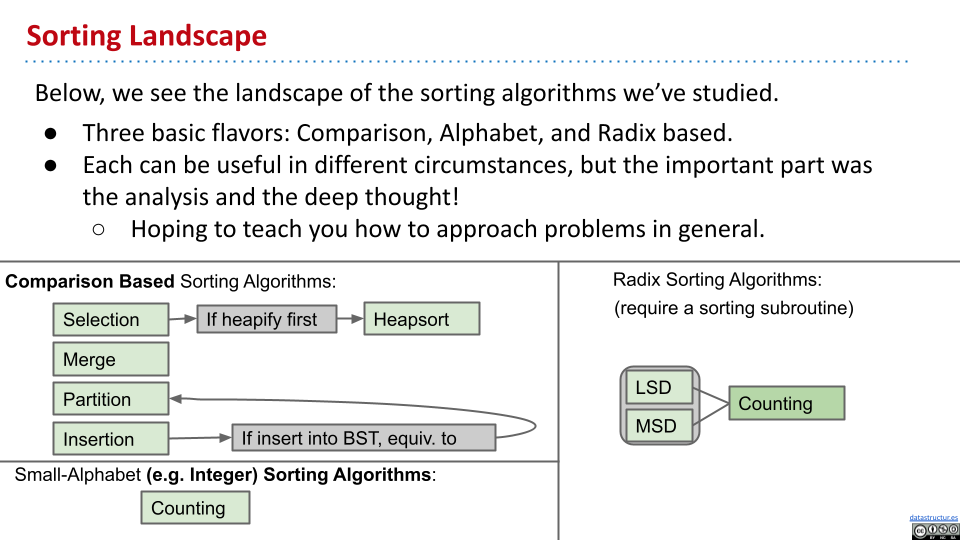
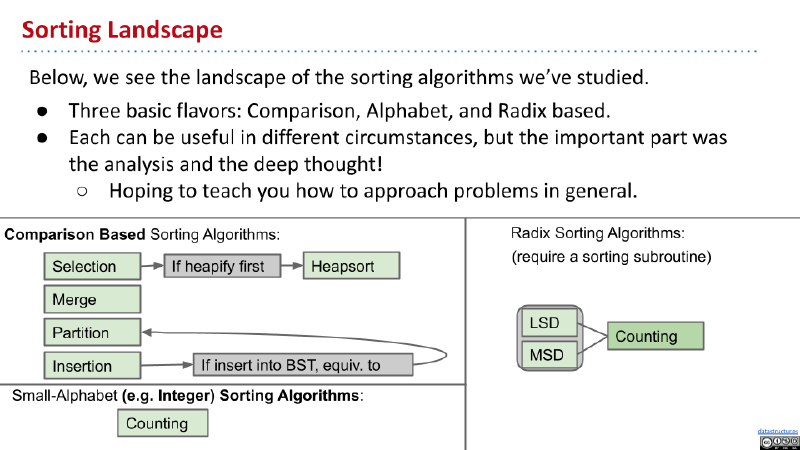
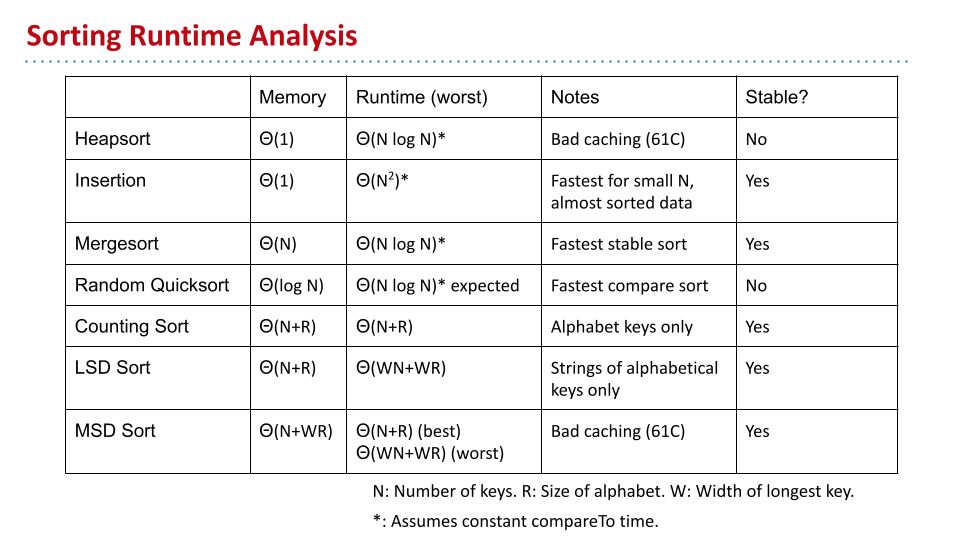
排序总结
排序部分的总结如下: