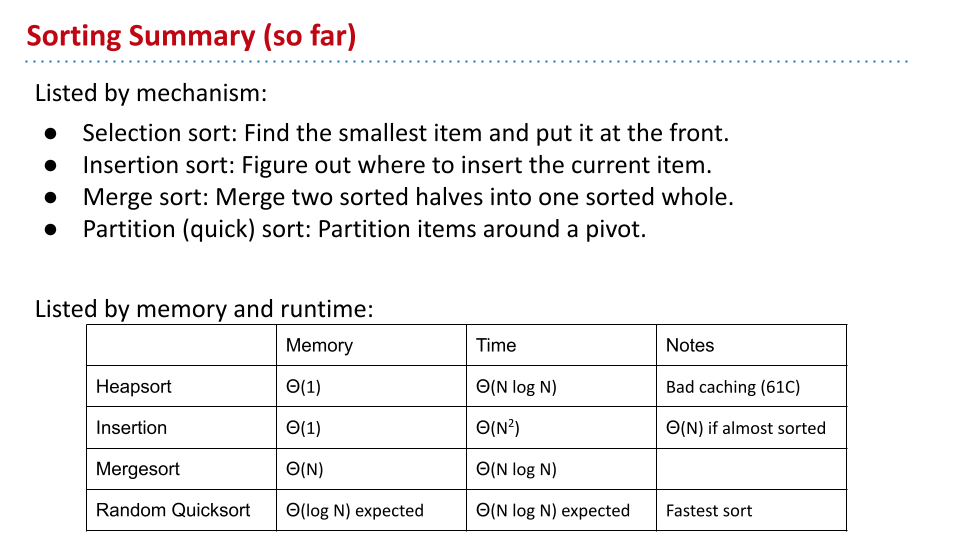
lec32 More Quick Sort, Sorting Summary
避免最坏情况
随机性
在最坏情况下,快速排序的表现不好。为了避免这种情况,可以引入随机性,随机选择 pivot 元素。
就地交换
如果使用扫描三次的方法,耗时较多。使用双指针,从左右两侧向中间扫描元素,这样可以让快速排序更快。
找到中位数
可以使用 BFPRT 方法,使用 $\Theta(n)$ 的时间找到一个数组中的中位数。但是,在实践中很少使用。
使用 partitioning 的思想,每次分组之后,对于不包括中间元素的部分剪枝,对剩下的部分进行 partitioning。
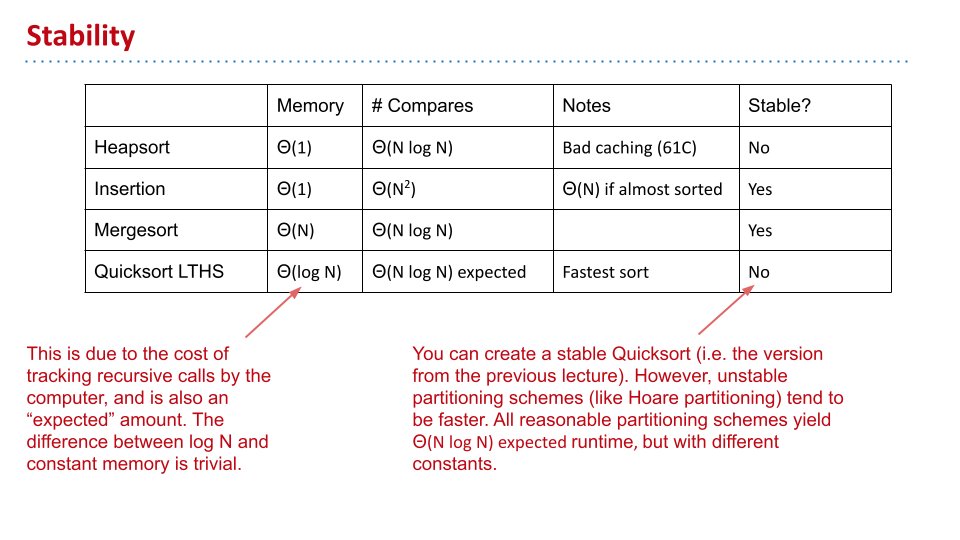
稳定性
如果原先相同值的顺序保持不变,那么就有稳定性。
在插入排序中,相同值的数不会改变顺序,具有稳定性。在快速排序中,扫描三次具有稳定性,但是使用双指针没有稳定性。
lec33 Software Engineering III
这一讲比较水,略过。
lec34 Sorting and Algorithmic Bounds
排序
排序在很多地方有用。例如要寻找数组中的重复元素,如果使用排序,就可以让复杂度从 $O(n^2)$ 降到 $O(n\log(n))$。又比如在三数之和等问题中有用。
通过数学,可以证明 $\log(n!)$ 是 $n\log(n)$ 的同阶无穷大。
假设拥有最快的排序算法,那么它的运行时间一定是 $O(n\log(n))$。同时,最差情况下,至少要遍历所有元素,才能确认是排序的。所以运行时间为 $\Omega(n)$。
小狗、猫和大狗
假设把小狗、猫和大狗放进不透明的三个盒子当中,你只有一个秤。怎么样来判断?
有些情况下,只需要两次比较就可以。但是,有些情况下,进行两次比较之后,必须进行第三次比较。
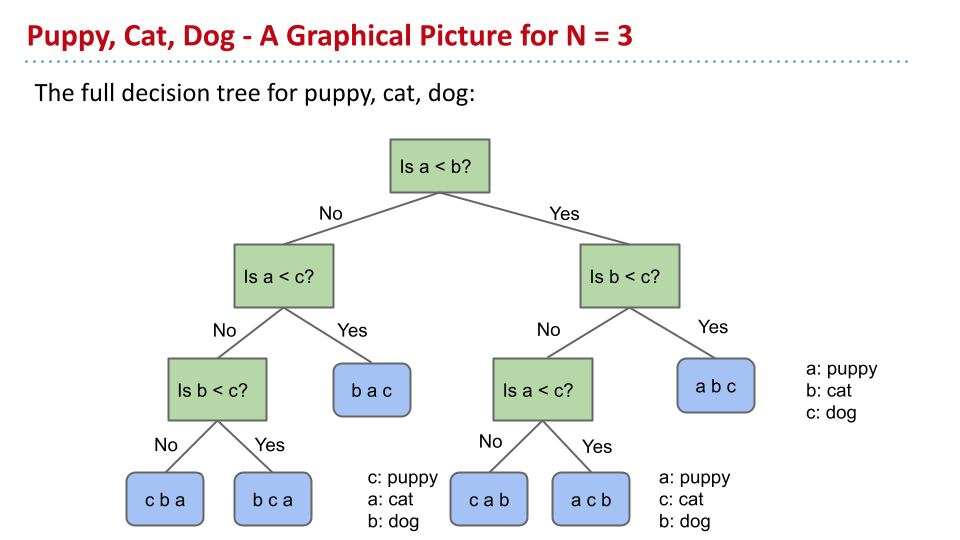
假设有四个物品,那么最多需要几次比较?答案是 5。此时,所有的排序为 $4!=24$,树上有 24 个叶子,又因为 $\log_2(24)=4.5$,所以 5 是最小值。
对于 $n$ 个物品,至少需要 $\Omega(\log(n!))$ 次判断,才能判断顺序。同时,你也可以先对这些物品排序,然后可以确定顺序。
排序是解决这个问题的一种方式。而这个问题拥有 $\Omega(\log(n!))$ 的判断条件,所以排序问题也是 $\Omega(\log(n!))$。又因为排序时间的上界为 $O(n\log(n))$,所以可以证明最好的排序时间为 $\Theta(n\log(n))$。
