lec26 Prefix Operations and Tries
引入
对于 Map 和 Set，已经讨论过了多种实现方式，包括平衡二叉树和哈希表。不过，其实还有其他方式来实现。
字符的 keyed map
例如对于 ASCII 字符，可以使用数组。索引为对应的 ASCII 吗，值为对应的字符。显然，时间复杂度为 $\Theta(1)$。
String 的 keyed map
在 trie 中，每个节点储存一个字符。如果是蓝色，则代表这个路径的单词存在；如果是白色，则代表不存在。
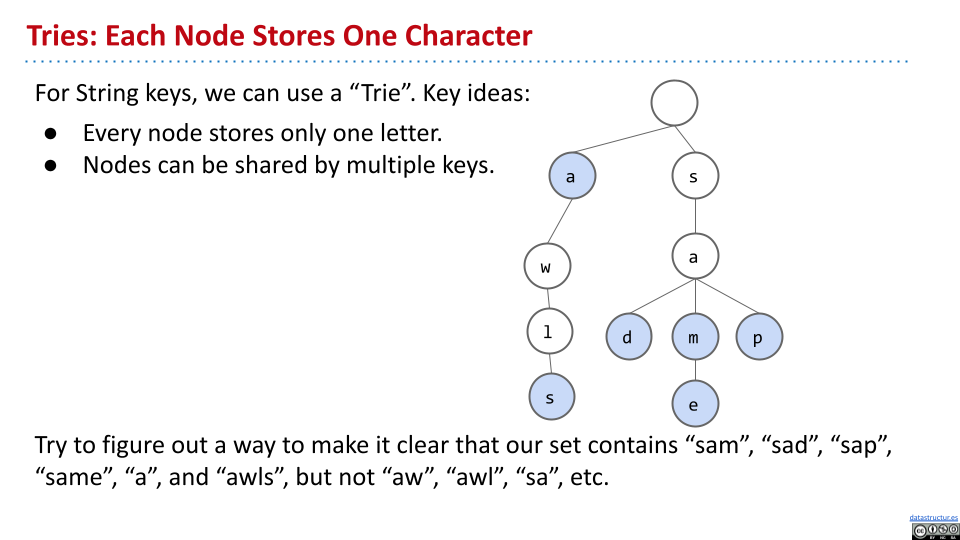
搜索
在搜索的时候，如果当前字符不在 trie 中，就说明不存在。或者最后一个字符在 trie 中，但是节点是白色，说明该字符串不存在。
Trie 的实现与性能
实现
实现方法如下：
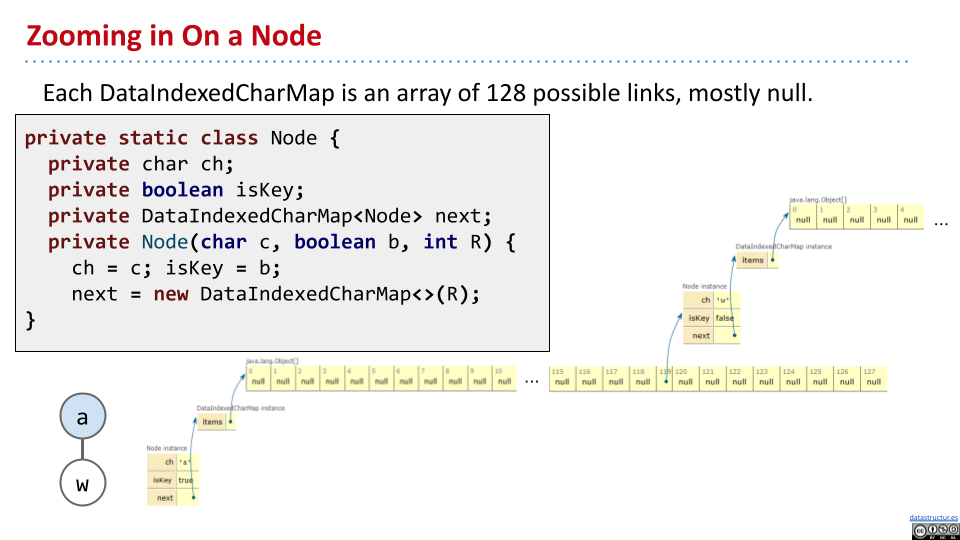
可以发现，这当中储存的 ch 实际上是多余的。可以仅仅根据对应索引来得到字符。
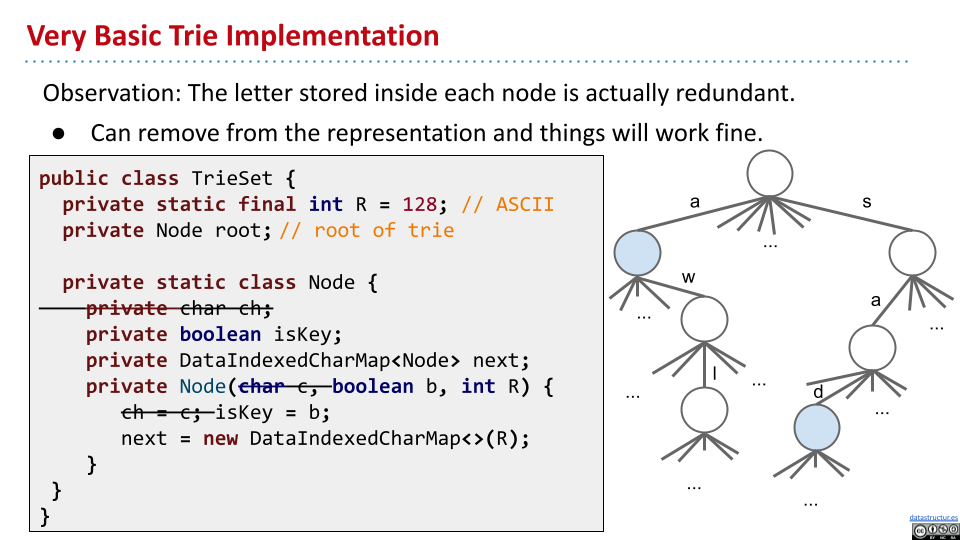
性能
对于字符串个数 N 来说，Trie 中 add 的时间为 $\Theta(1)$ ，contains 操作也为 $\Theta(1)$。对于字符串长度 L 来说，add 操作为 $\Theta(L)$ ，contains 操作为 $O(L)$。
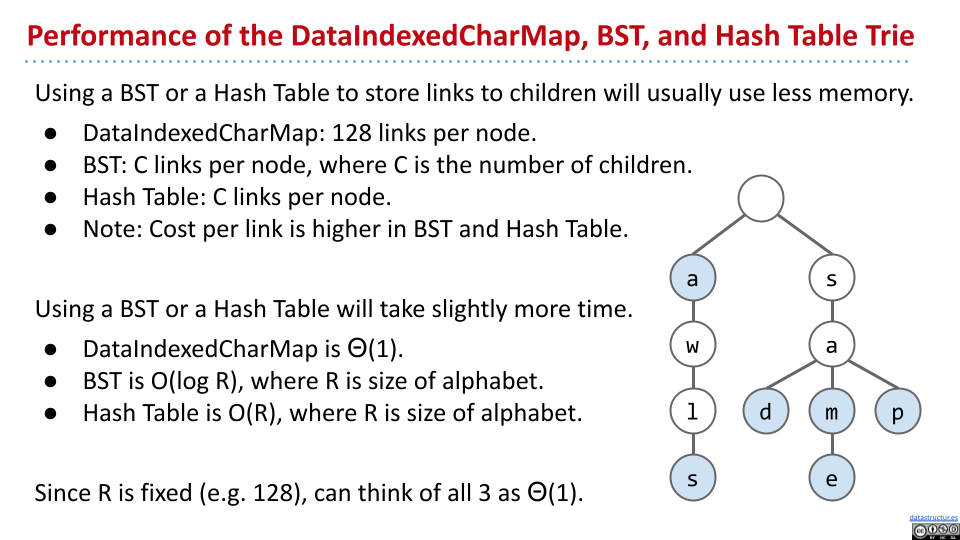
不同数据结构的性能比较如下：
然而，trie 的缺点也很明显，那就是有很多无效的链接，空间消耗较多。
其他方法
哈希表
为了避免大量无效的链接，使用哈希表。
二叉树
使用二叉树来表示链接的部分。
字符串操作
找到所有字符串
通过递归，不断调用子节点，收集字符串。
找拥有前缀的字符串
对于 Trie 来说，比较好用的性质就是得到拥有某一前缀的单词，或者根据某一单词找到最大拥有的前缀。
首先根据前缀，找到初始节点，然后调用 colHelp()。
自动补全
利用字典树，构造从字符串到重要程度的 Map。利用前缀的性质，可以很方便地实现。
为了优化算法，每个节点不仅仅储存自身的值，还储存子节点中最优的值。同时利用 PQ。
对于没有分支的一串节点，可以压缩成一个节点。这成为 radix tree 或者 radix trie。
lec27 Software Engineering I
复杂性
引入
和其他工程原则不同，软件并不是通过物理原则来限制的。很多时候，最大的限制是要清楚我们在创造什么，也就是创造力。
有一些 IDE 工具，调试器，可视化工具等，可以帮助处理复杂性。但是，最重要的原则是保持简单。
有两种方式来管理复杂性：
- 让代码简单、明显（例如使用虚拟头结点来减少特殊情况）
- 封装，模块化
本质
复杂性就是任何让人难以理解和修改系统的软件结构。在代码中，例如过多的条件判断，过多的缩进层次等，都会难以理解。
如果一小部分的代码相当复杂，但是其他人几乎不会看这些部分，那么总的影响很小。
症状
- 修改难度：一个简单的改变，需要在多个地方更改。
- 认知难度：要进行一个更改，需要知道多少。
- 有时候代码更多，分成小部分，更容易理解。
- 增加变量说明用途，也能减小认知难度。
- 未知的未知：甚至不知道需要知道什么，才能进行修改
分析
一开始，程序都是清晰、简单的。但是随着进展，逐渐变得丑陋。许多微妙的互相关联，会导致之后难以修改。尽量每一次更改都要尽可能简洁。
编程方式
战术式编程
- 不花时间自考整体的设计
- 增加了许多细小的复杂性
- 每一个复杂性看上去很小，但总体却很大
战略性编程
仅仅可以跑的代码是不够的。
- 最重要的是长远的系统结构
- 不能为了短期而增加复杂性
对于每一个新的类或者任务：
- 不要只是实现第一想法，而是尝试一些其他想法
- 当你觉得一些方法很清晰，就实现它
- 在现实系统中：思考在未来事情可能需要哪些改变，确保你的设计考虑了这些改变
然而，战略性编程也相当难。需要思考设计，同时也很难真正提前设计复杂的软件系统。
lec28 Reductions and Decomposition
拓扑排序
在有向图中，箭头表示前者必须在后者之前发生。如何找到一种排序，满足这种限制？
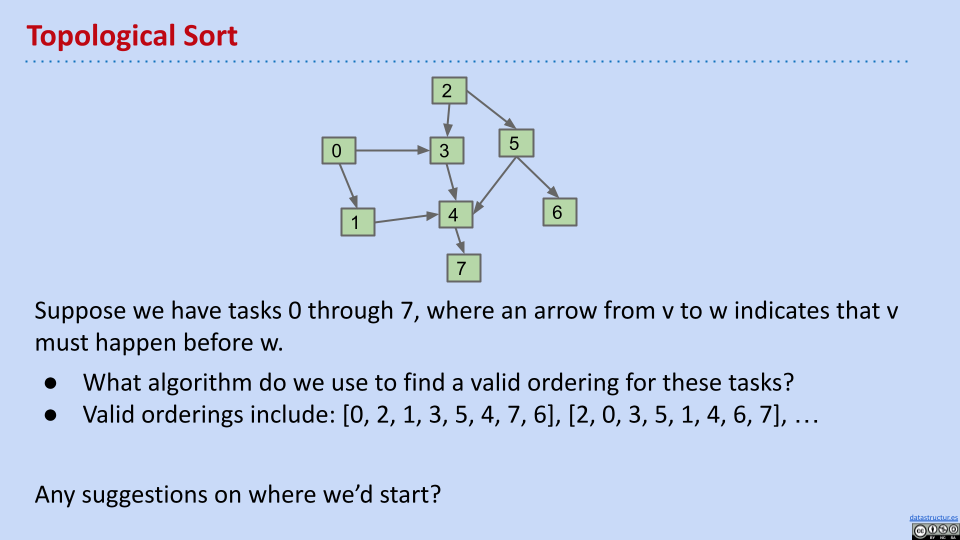一开始，可能认为先找到所有“根节点”，也就是没有被指向的节点，然后同时使用 BFS。
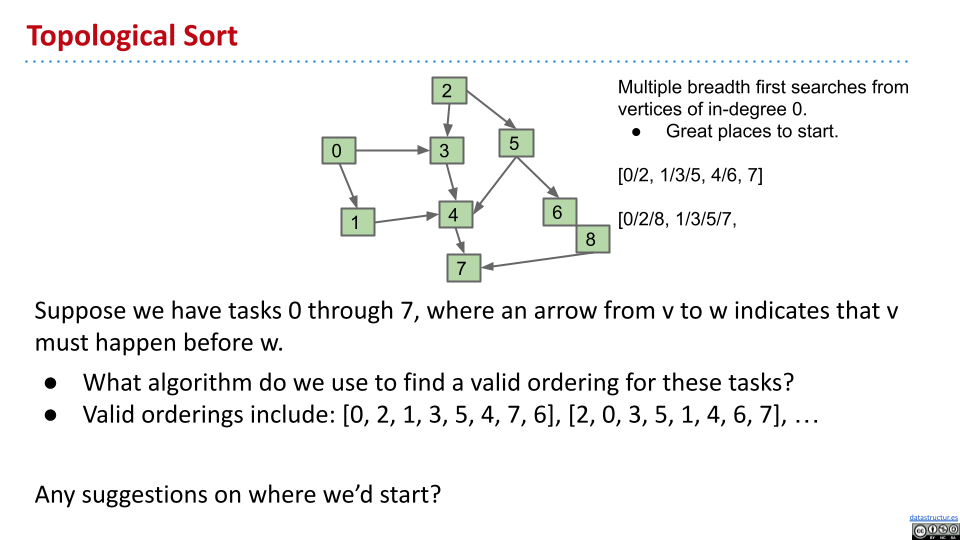然而，图稍微变一下，这个方法就不适用了。
考虑从起点开始使用 DFS，利用后序记录数字。保留所有标记。然后从另一个起点开始使用后序 DFS，补充在一开始列表的后面。最后翻转列表，得到结果。
之后，得到的列表中，指针方向都是向右的。
该算法也不一定从头结点开始。可以选择随机的节点，DFS 后，从没有标记的节点中随机选，直到全部标记。
DAG 的最短路径
DAG 也就是有向无环图。这类图肯定可以拓扑排序。
正如之前所说，如果有负值，此时 Dijkstra 可能会失效。为了解决这个问题，先利用拓扑排序，然后利用拓扑排序的顺序来遍历节点，更新每个边。
最长路径
在一般的图当中，没有适用的好算法，只有指数增长的算法。这是一个还没有解决的数学难题。
DAG 上的最长路径
只要把值翻转就行。然后，使用 DAG 上的最短路径即可。
Reduction
在刚刚的问题中，通过翻转符号，让 DAG 上最长路径问题，转换为了最短路径问题，之后再变换回来，问题得到了解决。这叫做“归约”。